题目内容
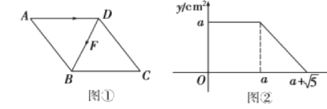
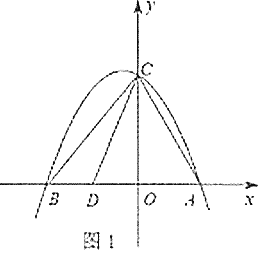
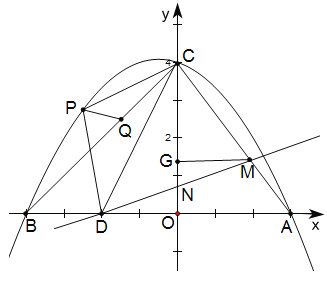
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,且点
,且点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() .
.
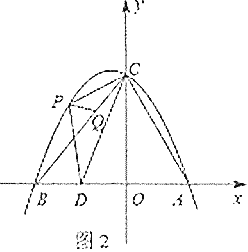
(1)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一动点,在线段
上方抛物线上的一动点,在线段![]() 上有一动点
上有一动点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)将过点![]() 的直线
的直线![]() 绕点
绕点![]() 旋转,设旋转中的直线
旋转,设旋转中的直线![]() 分别与直线
分别与直线![]() 、直线
、直线![]() 交于点
交于点![]() 、
、![]() ,当
,当![]() 为等腰三角形时,直接写出
为等腰三角形时,直接写出![]() 的长.
的长.
【答案】(1)![]() 的最小值为
的最小值为![]() ;(2)当
;(2)当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.
【解析】
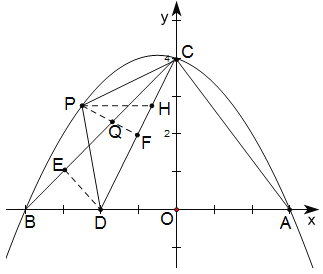
(1)首先求出点A、B、C、D的坐标及直线CD解析式,然后连接PC,PD,过点P作PH∥x轴交CD于H,设P(x,![]() ),则H(
),则H(![]() ,
,![]() ),列出
),列出![]() 面积的二次函数表达式,根据二次函数的性质求出
面积的二次函数表达式,根据二次函数的性质求出![]() 面积的最大值及此时P点的坐标,过点D作DE⊥BC于E,求出sin∠DCE=
面积的最大值及此时P点的坐标,过点D作DE⊥BC于E,求出sin∠DCE=![]() ,再过点Q作QF⊥CD于F,根据sin∠QCF=
,再过点Q作QF⊥CD于F,根据sin∠QCF=![]() ,可得
,可得![]() ,则
,则![]() ,进而得到当P、Q、F三点共线时,
,进而得到当P、Q、F三点共线时,![]() 的值最小,此时PF⊥CD,PF为
的值最小,此时PF⊥CD,PF为![]() 的最小值,最后利用面积法求出PF即可;
的最小值,最后利用面积法求出PF即可;
(2)当CM=CN时,过点M作MG∥x轴,可得△CGM∽△COA,设GM=3a,则CG=4a,CM=5a,根据CM=CN可求出GN=a,然后由平行得出△MGN∽△DON,根据相似三角形的性质求出ON,即可得到CM=CN的值,当CM=MN和CN=MN时,同理可得答案.
解:(1)在抛物线![]() 中,令y=0,即
中,令y=0,即![]() ,
,
解得:![]() ,
,![]() ,
,
∴B(-4,0),A(3,0),
令x=0,则![]() ,
,
∴C(0,4),
∵点![]() 是线段
是线段![]() 的中点,
的中点,
∴D(-2,0),
设直线CD解析式为:y=kx+4(k≠0),
代入(-2,0)得:0=-2k+4,
解得:k=2,
∴直线CD解析式为:y=2x+4,
如图,过点P作PH∥x轴交CD于H,
设P(x,![]() ),则H(
),则H(![]() ,
,![]() ),
),
∴PH=![]() ,
,
∴![]() ,
,
∴当x=![]() 时,
时,![]() 面积的最大值为
面积的最大值为![]() ,
,
把x=![]() 代入
代入![]() 得:
得:![]() ,
,
∴P(![]() ,
,![]() ),
),
∵OB=OC=4,
∴∠CBO=45°,
过点D作DE⊥BC于E,则△BED是等腰直角三角形,
∵BD=2,
∴BE=DE=![]() ,
,
∵CD=![]() ,
,
∴在Rt△DCE中,sin∠DCE=![]() ,
,
过点Q作QF⊥CD于F,
在Rt△QCF中,sin∠QCF=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当P、Q、F三点共线时,![]() 的值最小,此时PF⊥CD,PF为
的值最小,此时PF⊥CD,PF为![]() 的最小值,
的最小值,
∴![]() ,
,
∴![]() ,
,
即当![]() 面积最大时,
面积最大时,![]() 的最小值为
的最小值为![]() ;
;
(2)由(1)知,OA=3,OC=4,
∴AC=5,
如图,当CM=CN时,过点M作MG∥x轴,
则△CGM∽△COA,
∴![]() ,即
,即![]() ,
,
设GM=3a,则CG=4a,CM=5a,
∴CN=CM=5a,
∴GN=a,
∵MG∥AD,
∴△MGN∽△DON,
∴![]() ,
,
∵OD=2,
∴ON=![]() ,
,
∴CM=CN=![]() ;
;
当CM=MN时,同理可得CM=![]() ,
,
当CN=MN时,同理可得CM=![]() ,
,
综上所述,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为
的长为![]() 或
或![]() 或
或![]() .
.

【题目】某区正在积极创建国家模范卫生城市,学校为了普及学生卫生健康知识,提高学生创卫意识,举办了创卫知识竞赛,以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:75 88 93 65 78 94 89 68 95 50 89 88 89 89 77 95 87 88 92 91
初二:74 96 96 89 97 74 69 76 72 78 99 72 97 85 98 74 89 73 98 74
(1)整理、描述数据:
成绩 |
|
|
|
|
|
初一(频数) | 1 | 2 | 3 |
| 6 |
初二(频数) | 0 | 1 | 9 | 3 | 7 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下不合格)
分析数据:
平均数 | 中位数 | 众数 | |
初一 | 84 |
| 89 |
初二 | 84 | 81.5 |
|
请根据上述的数据,填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)得出结论:
你认为哪个年级掌握创卫知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
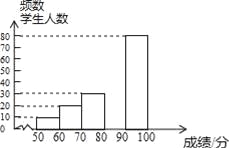
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?