题目内容

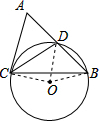
如图，⊙O为△BCD的外接圆，过C点作⊙O的切线交BD的延长线于A，∠ACB=75°，∠ABC=45°，则
CD
DB
的值为（　　）
A．
3
2
B．2C．
2
D．
2
2
设圆的半径为r，连接OB，OC，OD，
∵AC为⊙O的切线，
∴∠DCA=∠CBD=45°，
∴∠BCD=∠BCA-∠DCA=75-45=30°，
∴∠BOD=2∠BCD=60°，
∴△BOD是等边三角形，BD=r，
∵∠CBD=45°，
∴∠COD=90°，
∴CD=
2
OC=
2
r，
∴
CD
DB
=
2
．
故选C．
练习册系列答案
相关题目
已知：如图，⊙A与y轴交于C、D两点，圆心A的坐标为（1，0），⊙A的半径为
5
，过C作⊙A的切线交x轴于点B．
（1）求切线BC的解析式；
（2）若点P是第一象限内⊙A上的一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP=120°，求点G的坐标；
（3）向左移动⊙A（圆心A始终保持在x轴上），与直线BC交于E、F，在移动过程中是否存在点A，使△AEF是直角三角形？若存在，求出点A的坐标；若不存在，请说明理由．
如图，BD是⊙O的直径，AB与⊙O相切于点B，过点D作OA平行线交⊙O于点C，AC与BD的延长线相交于点E．
（1）试探究AE与⊙O的位置关系，并说明理由；
（2）已知EC=a，ED=b，AB=c，请你思考后，选用以上适当的数据，计算⊙O的半径r．
已知PAB、PCD为⊙O的两条割线，PA=8，AB=10，CD=7，∠P=60°，则⊙O的半径为______．
如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠D=30°，
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，求
BC
的长．（结果保留π）
同学们都学习过《几何》课本第三册第199页的第11题，它是这样的：
如图，A为⊙O的直径EF上的一点，OB是和这条直径垂直的半径，BA和⊙O相交于另一点C，过点C的切线和EF的延长线相交于点D，求证：DA=DC．

（1）现将图1中的直径EF所在直线进行平行移动到图2所示的位置，此时OB与EF垂直相交于H，其它条件不变．
①求证：DA=DC；
②当DF：EF=1：8，且DF=
2
时，求AB•AC的值．
（2）将图2中的EF所在直线继续向上平行移动到图3所示的位置，使EF与OB的延长线垂直相交于H，A为EF上异于H的一点，且AH小于⊙O的切线交EF于D，试猜想：DA=DC是否仍然成立？证明你的结论．
如图1，平行四边形ABCD的对角线AC，BD交于点P，E为BC的中点，过E点的圆O与BD相切于点P，圆O与直线AC，BC分别交于点F，G．
（1）求证：△PCD∽△EPF；
（2）如果AB=AD，AC=6，BD=8（如图2）．求圆O的直径．
如图，AB切⊙O于点B，OA=2
3
，AB=3，弦BC∥OA，则劣弧BC的弧长为______．
如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网