题目内容
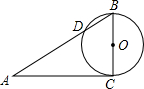
已知PAB、PCD为⊙O的两条割线，PA=8，AB=10，CD=7，∠P=60°，则⊙O的半径为______．
∵PA•PB=PC•PD，得8×18=PC•（PC+7），
解得：PC=9，
连接BC，
∵PB=2PC，∠P=60°，
∴∠BCP=90°，
∴∠BCD=90°，
连接BD，
∵∠BCD=90°，
∴BD为直径，
BD=
=
=2
．
故⊙O的半径为：
．
解得：PC=9，
连接BC，
∵PB=2PC，∠P=60°，
∴∠BCP=90°，
∴∠BCD=90°，
连接BD，
∵∠BCD=90°，
∴BD为直径，
BD=
| CD2+BC2 |
72+(9
|
| 73 |
故⊙O的半径为：
| 73 |
练习册系列答案
出彩同步大试卷系列答案
相关题目
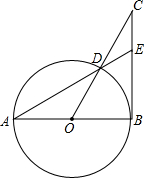
交⊙O1于点C．
∠DAB，延长AB交DC于点E．
