题目内容
如图，AB切⊙O于点B，OA=2
，AB=3，弦BC∥OA，则劣弧BC的弧长为______．
| 3 |
连接OB，OC，如图所示：
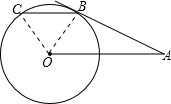
∵AB与圆O相切，
∴OB⊥AB，
∴∠ABO=90°，
在Rt△ABO中，OA=2
，AB=3，
根据勾股定理得：OB=
=
，
∴OB=
OA，
∴∠A=30°，
∴∠A0B=60°，
∵BC∥OA，
∴∠OBC=∠AOB=60°，又OB=OC，
∴△OBC为等边三角形，
∴∠BOC=60°，
则
的长l=
=
．
故答案为：
．
∵AB与圆O相切，
∴OB⊥AB，
∴∠ABO=90°，
在Rt△ABO中，OA=2
| 3 |
根据勾股定理得：OB=
| OA2-AB2 |
| 3 |
∴OB=
| 1 |
| 2 |
∴∠A=30°，
∴∠A0B=60°，
∵BC∥OA，
∴∠OBC=∠AOB=60°，又OB=OC，
∴△OBC为等边三角形，
∴∠BOC=60°，
则
 |
| BC |
60•π•
| ||
| 180 |
| ||
| 3 |
故答案为：
| ||
| 3 |
练习册系列答案
相关题目
交⊙O1于点C．
