题目内容
如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA平行线交⊙O于点C,AC与BD的延长线相交于点E.
(1)试探究AE与⊙O的位置关系,并说明理由;
(2)已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,计算⊙O的半径r.

(1)试探究AE与⊙O的位置关系,并说明理由;
(2)已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,计算⊙O的半径r.

(1)AC与⊙O相切.
其理由是:连接OC.
∵OC=OD,
∴∠CDO=∠DCO.
∵DC∥AO,
∴∠AOB=∠CDO,∠DCO=∠COA
∴∠COA=∠BOA.
在△ACO和△ABO中,
∵
,
∴△ACO≌△ABO(SAS),
∴∠ACO=∠ABO.
∵AB与⊙O相切,
∴∠ABO=90°,
∴∠ACO=90°,即OC⊥AC.
∴AE与⊙O相切;
(2)答案不唯一
①选a、b、c
∵AC、AB⊙O的切线
∴AC=AB=c.
∵DC∥AO
∴
=
,
∴
=
,
∴OD=
,即r=
(10分)
②选a、b,用勾股定理建方程,也可求得r=
(参照方法①给分)
其理由是:连接OC.
∵OC=OD,
∴∠CDO=∠DCO.
∵DC∥AO,
∴∠AOB=∠CDO,∠DCO=∠COA
∴∠COA=∠BOA.
在△ACO和△ABO中,
∵
|
∴△ACO≌△ABO(SAS),
∴∠ACO=∠ABO.
∵AB与⊙O相切,
∴∠ABO=90°,
∴∠ACO=90°,即OC⊥AC.
∴AE与⊙O相切;
(2)答案不唯一
①选a、b、c
∵AC、AB⊙O的切线
∴AC=AB=c.
∵DC∥AO
∴
| EC |
| AC |
| ED |
| OD |
∴
| a |
| c |
| b |
| OD |
∴OD=
| bc |
| a |
| bc |
| a |
②选a、b,用勾股定理建方程,也可求得r=
| a2-b2 |
| 2b |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目




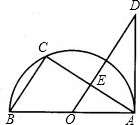 点D,且∠D=∠BAC.
点D,且∠D=∠BAC.
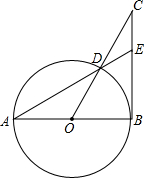
 交⊙O1于点C.
交⊙O1于点C.