Question

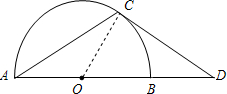
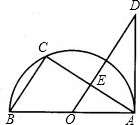
如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠D=30°，
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，求

BC

的长．（结果保留π）

Answer 1

（1）证明：连接OC，
∵AC=CD，∠D=30°，
∴∠A=∠D=30°，
∵OA=OC，
∴∠A=∠ACO=30°，
∴∠DOC=∠A+∠ACO=60°，
∴∠OCD=180°-30°-60°=90°，
∴OC⊥CD，
∵OC为⊙O半径，
∴CD是⊙O的切线；

（2）∵⊙O半径是3，∠BOC=60°，
∴由弧长公式得：

BC

的长为：

60π×3

180

=π．