Question

【题目】如图，在平面直角坐标系中，圆M经过原点O，直线y=﹣ x﹣6与x轴、y轴分别相交于A，B两点．

（1）求出A，B两点的坐标；
（2）若有一抛物线的对称轴平行于y轴且经过点M，顶点C在圆M上，开口向下，且经过点B，求此抛物线的函数解析式；
（3）设（2）中的抛物线交x轴于D、E两点，在抛物线上是否存在点P，使得
S△PDE= S△ABC？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：对于直线y=﹣ x﹣6，

当x=0，y=﹣6；

当y=0，得0=﹣ x﹣6，解得x=﹣8．

故A（﹣8，0），B（0，﹣6）；

（2）

解：在Rt△AOB中，AB= =10，

∵∠AOB=90°，

∴AB为⊙M的直径，

∴点M为AB的中点，M（﹣4，﹣3），

∵MC∥y轴，MC=5，

∴C（﹣4，2），

设抛物线的解析式为y=a（x+4）2+2，

把B（0，﹣6）代入得16a+2=﹣6，解得a=﹣ ，

∴抛物线的解析式为y=﹣ （x+4）2+2，即y=﹣ x2﹣4x﹣6，

（3）

解：存在．

如图，

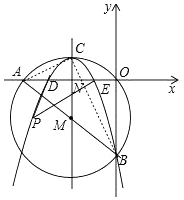
当y=0时，﹣ （x+4）2+2=0，解得x1=﹣2，x2=﹣6，

∴D（﹣6，0），E（﹣2，0），

S△ABC=S△ACM+S△BCM= ×CM×8=20，

设P（t，﹣ x2﹣4x﹣6），

∵S△PDE= S△ABC，

∴ （﹣2+6）|﹣ t2﹣4t﹣6|= ×20，

即|﹣ t2﹣4t﹣6|=1，

当﹣ t2﹣4t﹣6=﹣1，解得t1=﹣4+ ，t2=﹣4﹣ ，此时P点坐标为（﹣4+ ，﹣1）或（﹣4﹣ ，﹣1）；

当﹣ t2﹣4t﹣6=1，解得t1=﹣4+ ，t2=﹣4﹣ ，此时P点坐标为（﹣4+ ，1）或（﹣4﹣ ，1）．

综上所述，P点坐标为（﹣4+ ，﹣1）或（﹣4﹣ ，﹣1）或（﹣4+ ，1）或（﹣4﹣ ，1）时，使得S△PDE= S△ABC．

【解析】（1）根据一次函数与坐标轴交点坐标求法得出答案即可；（2）利用顶点式由B点坐标求出二次函数解析式即可；（3）首先求出△ABC的面积，进而求出D，E坐标，设P（t，﹣ x2﹣4x﹣6），根据S△PDE= S△ABC ， 得到|﹣ t2﹣4t﹣6|=1，分两种情况讨论即可求出P点坐标．
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．