Question

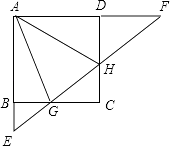
【题目】如图，已知点P是⊙O外一点，PB切⊙O于点B，BA 垂直OP于C，交⊙O于点A，连接PA、AO，延长AO，交⊙O于点E．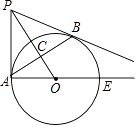
（1）求证：PA是⊙O的切线；
（2）若tan∠CAO= ，且OC=4，求PB的长．

Answer 1

【答案】
（1）证明：连接OB，则OA=OB，

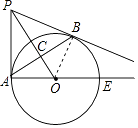
∵OP⊥AB，∴AC=BC，∴OP是AB的垂直平分线，∴PA=PB，

在△PAO和△PBO中，

∵ ，

∴△PAO≌△PBO（SSS），

∴∠PAO=∠PBO，

∵PB为⊙O的切线，B为切点，

∴∠PBO=90°，

∴∠PAO=90°，即PA⊥OA，

∴PA是⊙O的切线；

（2）解：∵tan∠CAO= = ，且OC=4，

∴AC=6，

∴AB=12

在Rt△ACO中，AO= = =2 ．

显然△ACO∽△PAO，

∴ = ，即 = ，

∴PA=3 ，

∴PB=PA=3 ．

【解析】（1）证明△PAO≌△PBO，根据全等三角形的对应角相等证得∠PAO=∠PBO，则∠PBO=90°，根据切线的判定定理证得；（2）在Rt△ACO中，利用勾股定理求得OA的长，然后根据△ACO∽△PAO，利用相似三角形的对应边的比相等求解．
【考点精析】认真审题，首先需要了解解直角三角形(解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法))．