题目内容
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=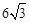 ,OE=3;
,OE=3;

求:
(1)⊙O的半径;
(2)阴影部分的面积。
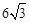 ,OE=3;
,OE=3;
求:
(1)⊙O的半径;
(2)阴影部分的面积。
(1)6;(2) .
.
 .
.试题分析:(1)利用垂径定理求得CE=
 ,在Rt△COE中,由勾股定理求得CO的长度;
,在Rt△COE中,由勾股定理求得CO的长度;(2)阴影部分的面积=扇形ACO的面积-△AOC的面积.
试题解析:(1)∵BC是⊙O的弦,半径OD⊥BC,BC=
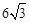 ,∴CE=
,∴CE= BC=
BC= .
.∴在Rt△COE中,由勾股定理得,
 ,
,∴⊙O的半径是6.
(2)∵在Rt△COE中,∠CEO=90°,CO=2OE,∴∠ECO=30°.
∵AB是⊙O的直径,∴∠ACB=90°.∴∠ACO=60°.
∵OA=OC,∴△ACO是等边三角形.∴∠AOC=60°.
∴S阴影=S扇形ACO-S△AOC=
 .
.答:阴影部分的面积是
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 ,AD=4,求AB的长.
,AD=4,求AB的长.

 ,若∠BEC=110°,则∠BDC( )
,若∠BEC=110°,则∠BDC( )

 ,且∠A=60°,半径OB=2,则下列结论不正确的是( )
,且∠A=60°,半径OB=2,则下列结论不正确的是( )
 的度数为240°
的度数为240°
