题目内容
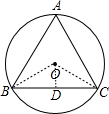
如图, ,且∠A=60°,半径OB=2,则下列结论不正确的是( )
,且∠A=60°,半径OB=2,则下列结论不正确的是( )

 ,且∠A=60°,半径OB=2,则下列结论不正确的是( )
,且∠A=60°,半径OB=2,则下列结论不正确的是( )
| A.∠B=60° | B.∠BOC=120° |
C. 的度数为240° 的度数为240° | D.弦BC= |
D.
试题分析:作OD⊥BC于D,连结OB、OC,根据圆周角定理得到∠B=∠C=60°,∠BOC=2∠A=120°,在根据圆心角、弦、弧的关系得到
 的度数为240°;由OD⊥BC,利用垂径定理得BD=CD,再利用含30度的直角三角形三边的关系可计算出BC.
的度数为240°;由OD⊥BC,利用垂径定理得BD=CD,再利用含30度的直角三角形三边的关系可计算出BC.作OD⊥BC于D,连结OB、OC,如图,
∵
 ,且∠A=60°,
,且∠A=60°,∴∠B=∠C=60°,∠BOC=2∠A=120°,
∴
 的度数为240°;
的度数为240°;∵OD⊥BC,
∴BD=CD,∠OBD=30°,
而OB=2,
∴OD=1,
∴BD=
 OD=
OD= ,
,∴BC=2BD=2
 .
.故选D.
考点: 1.圆周角定理;2.等边三角形的判定与性质;3.垂径定理;4.圆心角、弧、弦的关系.

练习册系列答案
相关题目
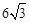 ,OE=3;
,OE=3;


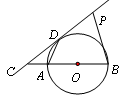

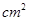 .
. ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .