题目内容
如图,⊙O是△ABC的外接圆,∠OBC=30°,则∠BAC的度数为__________。


60°.
试题分析:由OB=OC得到∠OCB=∠OBC=30°,根据三角形内角和定理计算出∠BOC=120°,然后根据圆周角定理求解.
试题解析:∵OB=OC,
∴∠OCB=∠OBC=30°,
∴∠BOC=180°-30°-30°=120°,
∴∠BAC=
 ∠BOC=60°.
∠BOC=60°.故答案为60°.
考点: 圆周角定理.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图所示,直线CD与线段AB为直径的圆相切于点D,并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP的度数为
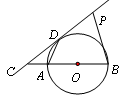

| A.90° | B.60° | C.45° | D.30° |

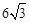 ,OE=3;
,OE=3;

 ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )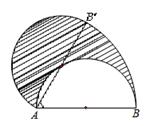
 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为 .