题目内容
如图.在平面直角坐标系中,边长为 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.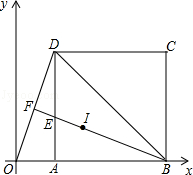
(1)求证:△OAD≌△EAB;
(2)求过点O、E、B的抛物线所表示的二次函数解析式;
(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;
(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.
解:(1)证明:如答图1所示,连接ID,IO,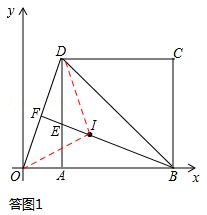
∵I为△BOD的外心,∴IO=ID。
又F为OD的中点,∴IF⊥OD。
∴∠DEF+∠FDE=∠AEB+∠ABE=90°。
又∠DEF=∠AEB,∴∠EDF=∠EBA。
又∵DA=BA,且∠OAD=∠EAB=90°,
∴△OAD≌△EAB(AAS)。
(2)由(1)知IF⊥OD,又BF为中线,
∴BO=BD= AB=2。∴OA=BO﹣AB=
AB=2。∴OA=BO﹣AB=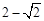 。
。
由(1)知△OAD≌△EAB,∴AE=OA=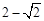 。
。
∴E(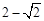 ,
,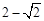 ),B(2,0)。
),B(2,0)。
设过点O、B、E的抛物线解析式为y=ax2+bx,
∴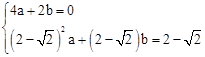 ,解得
,解得 。
。
∴抛物线的解析式为: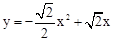 。
。
(3)∵直线BD与x轴关于直线BF对称,∴抛物线与直线BD的交点,即为所求之点P。
由(2)可知,B(2,0),D(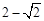 ,
, ),可得直线BD的解析式为y=﹣x+2。
),可得直线BD的解析式为y=﹣x+2。
∵点P既在直线y=﹣x+2上,也在抛物线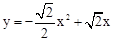 上,
上,
∴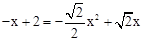 ,解得:x=2或x=
,解得:x=2或x= 。
。
当x=2时,y=﹣x+2=0;当x= 时,y=﹣x+2=
时,y=﹣x+2=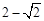 ,
,
∴点P的坐标为(2,0)(与点B重合),或( ,
,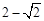 )。
)。
(4)∵DBO=45°,BD=BO,BF⊥OD,
∴∠EBA=22.5°。
由(1)知∠ODA=22.5°,
∴∠DOA=67.5°,OA=EA。
∴∠EOA=45°,∠DOE=22.5°
∴△OED是顶角为135°的等腰三角形。
若△BMD与△OED相似,则△BMD必须是等腰三角形。
如答图2所示,在直线BF上能使△BMD为等腰三角形的点M有4个,分别记为M1,M2,M3,M4,其中符合题意的是点M1,M3。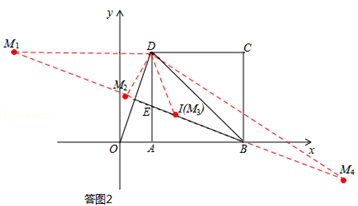
∵DM1=DB=2,OA=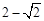 ,∴M1(
,∴M1(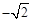 ,
, )。
)。
由(1)知B(2,0),E(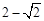 ,
,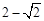 ),故直线BE的解析式为y=(1﹣
),故直线BE的解析式为y=(1﹣ )x﹣2+
)x﹣2+ 。
。
∵I是△BOD的外心,它是OB的垂直平分线x=1与OD的垂直平分线BE的交点,
∴I(1, ﹣1),即M3(1,
﹣1),即M3(1, ﹣1).
﹣1).
∴符合题意的M点的坐标为(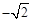 ,
, ),(1,
),(1, ﹣1)。
﹣1)。
解析试题分析:(1)连接ID,IO,通过证明IF⊥OD而得到∠FED=∠EBA;又由DA=BA,且∠OAD=∠EAB=90°,即可由AAS证得△OAD≌△EAB;
(2)求出点B、E的坐标,然后利用待定系数法求出抛物线的解析式。
(3)由于直线BD与x轴关于直线BF对称,则抛物线与直线BD的交点即为所求之点P。分别求出抛物线与直线BD的解析式,联立解方程,即可求出交点(点P)的坐标。
(4)首先证明△OED是顶角为135°的等腰三角形,若△BMD与△OED相似,则△BMD必须是等腰三角形.如答图2所示,在直线BF上能使△BMD为等腰三角形的点M有4个,分别记为M1,M2,M3,M4,其中符合题意的是点M1,M3。

 阅读快车系列答案
阅读快车系列答案 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象 .
.
 轴相交于点
轴相交于点 、点
、点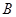 (点
(点 ,点
,点 位于
位于 轴负半轴上,且到
轴负半轴上,且到 所在直线的解析式.
所在直线的解析式. (a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程
(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程 的两根.
的两根.
 的对称轴是直线x=
的对称轴是直线x= ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
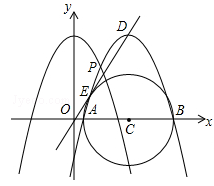
 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°, 。
。
 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.