题目内容
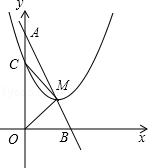
如图,抛物线 的对称轴是直线x=
的对称轴是直线x= ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
(1)求抛物线的解析式;
(2)过点C作CD//x轴交抛物线于点D,连接AD交y轴于点E,连接AC,设△AEC的面积为S1, △DEC的面积为S2,求S1:S2的值;
(3)点F坐标为(6,0),连接D,在(2)的条件下,点P从点E出发,以每秒3个单位长的速度沿E→C→D→F匀速运动;点Q从点F出发,以每秒2个单位长的速度沿F→A匀速运动,当其中一点到达终点时,另外一点也随之停止运动.若点P、Q同时出发,设运动时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是直角三角形?请直接写出所有符合条件的t值..
解:(1)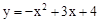
(2)
(3)当 时,以D、P、Q为顶点的三角形是直角三角形。
时,以D、P、Q为顶点的三角形是直角三角形。
解析试题分析:(1)由∵抛物线 的对称轴是直线x=
的对称轴是直线x= 和经过点A(—1,0),得
和经过点A(—1,0),得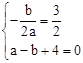 ,解之即可得抛物线的解析式。
,解之即可得抛物线的解析式。
∵抛物线 的对称轴是直线x=
的对称轴是直线x= ,∴
,∴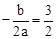 ①。
①。
又∵抛物线 经过点A(—1,0),∴
经过点A(—1,0),∴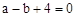 ②。
②。
联立①②,解得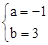 。
。
∴抛物线的解析式为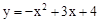 。
。
(2)根据相似三角形和等高三角形的性质,可得 和
和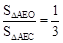 ,从而
,从而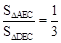 ,即S1:S2=
,即S1:S2= 。
。
在 中令x=0得
中令x=0得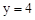 ,∴C(0,4)。
,∴C(0,4)。
∵抛物线 的对称轴是直线x=
的对称轴是直线x= ,CD//x轴交抛物线于点D,∴D(3,4)。
,CD//x轴交抛物线于点D,∴D(3,4)。
又OA=1,CD=3,
∵CD//x轴,∴△AEO∽△DEC。∴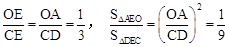 ③。
③。
又∵△AEO和△AEC是两等高三角形,∴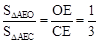 ④。
④。
③÷④,得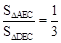 ,即S1:S2=
,即S1:S2= 。
。
(3)分四种情况讨论:
①当点P在EC上运动,∠PDQ=900时,如图1,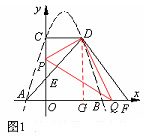
过点D作DG⊥AB于G,则CD=3,PC= 3—3t,GD=4,QG=3—2t,
由△PCD∽△QGD得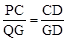 ,即
,即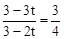 ,解得
,解得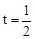 。
。
②当点P在CD上运动,∠PDQ=900时,如图2,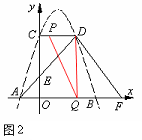
OQ=6—2t,CD=3,此时,OQDC是矩形。由OQ=CD,即6—2t=3解得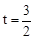 。
。
③当点P在CD上运动,∠QPD=900时,如图3,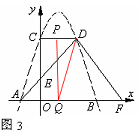
OQ=6—2t,CP=3t—3,此时,OQPC是矩形。由OQ=CP,6—2t=3t—3解得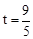 。
。
④当点P在DF上运动,∠QPD=900时,如图4,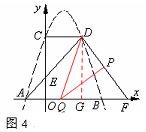
由D(3,4),F(6,0),根据勾股定理可得DF=5。
过点D作DG⊥AB于G,则DF=5,GF=3, PF= 11—3t, QF=2t,
由△FPQ∽△FGD得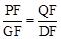 ,即
,即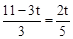 ,解得
,解得 。
。
综上所述,当 时,以D、P、Q为顶点的三角形是直角三角形。
时,以D、P、Q为顶点的三角形是直角三角形。


 (b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
 (元)与销售单价
(元)与销售单价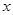 (元)之间的函数关系式;
(元)之间的函数关系式; 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.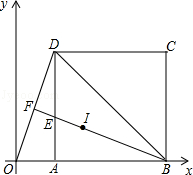
 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.