题目内容
已知,如图(a),抛物线 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°, 。
。
(1)求抛物线的解析式及顶点D的坐标;
(2)连结AD、BD,在(1)中的抛物线上是否存在一点P,使得△ABP与△ADB相似?若存在,求出P点的坐标;若不存在,说明理由;
(3)如图(b),点Q为 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
解:(1)圆的半径 ,
,
连接EM,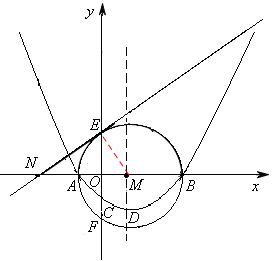
∵NE是⊙M的切线,∴ME⊥NE。
在Rt△MNE中,∠ONE=30°,MA=ME=4,
∴∠EMN=60°,MN=8。∴OM=2。
∴OA=2,OB=6。
∴点A、B的坐标分别为(―2,0),(6,0)。
∵抛物线经过点A、B两点,
∴设抛物线的解析式为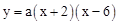 ,
,
又∵抛物线经过点C(0,-2),
∴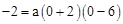 ,解得
,解得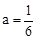 。
。
∴抛物线的解析式为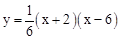 ,即
,即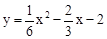 。
。
∵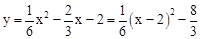 ,∴抛物线顶点D的坐标为(2,
,∴抛物线顶点D的坐标为(2,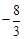 )。
)。
(2)如图,由抛物线的对称性可知:AD=BD,∠DAB=∠DBA。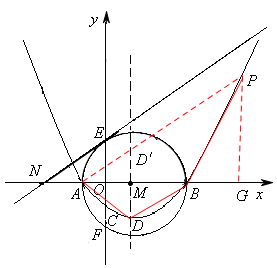
若在抛物线对称性的右侧图象上存在点P,使△ABP与△ADB相似,
必须有∠BAP=∠BPA=∠BPD。
设AP交抛物线的对称轴于D′点,则D′(2,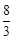 )。
)。
∴直线AP的解析式为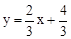 。
。
由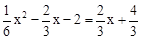 解得:
解得: (舍去)。
(舍去)。
∴P(10,8)。
过P作PG⊥x轴于点G,
在Rt△BGP中,BG=4,PG=8,
∴由勾股定理,得PB=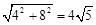 。
。
∵PA=8,∴PA≠PB。∴∠BAP≠∠BPA。
∴△ABP与△ADB不相似。
同理可说明在对称轴左边的抛物线上也不存在符合条件的P点。
∴在该抛物线上不存在点P,使得△ABP与△ADB相似。
(3)连接AF、QF,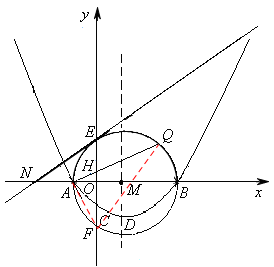
在△AQF和△AFH中,
由垂径定理易知: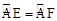 ,
,
∴∠AQF=∠AFH。
又∠QAF=∠HAF,
∴△AQF∽△AFH。
∴ ,∴
,∴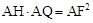 。
。
在Rt△AOF中,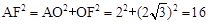 ,
,
∴AH·AQ=16,即:AH·AQ为定值
解析试题分析:(1)由切线的性质和含30度角直角三角形的性质,求出点A、B的坐标,从而应用待定系数法求出抛物线的解析式,化为顶点式即可得到抛物线的顶点D的坐标。
(2)应用反证法分抛物线对称性的右侧和抛物线对称性的左侧两种情况说明在该抛物线上不存在点P,使得△ABP与△ADB相似。
(3)由垂径定理和相似三角形的判定和性质,可得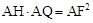 ,在Rt△AOF中,应用勾股定理可得
,在Rt△AOF中,应用勾股定理可得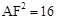 ,从而得出AH·AQ为定值的结论。
,从而得出AH·AQ为定值的结论。


 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.

 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.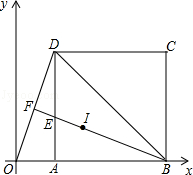


 的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
的顶点为点D,并与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
 ,0)和点F(0,
,0)和点F(0, ),直线l经过E、F两点,点G是线段BD的中点.
),直线l经过E、F两点,点G是线段BD的中点.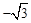 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).