题目内容
如图，在直角梯形AOCB中，AB∥OC，∠AOC=90°，AB=1，AO=2，OC=3，以O为原点，OC、OA所在直线为轴建立坐标系．抛物线顶点为A，且经过点C．点P在线段AO上由A向点O运动，点O在线段OC上由C向点O运动，QD⊥OC交BC于点D，OD所在直线与抛物线在第一象限交于点E．
（1）求抛物线的解析式；
（2）点E′是E关于y轴的对称点，点Q运动到何处时，四边形OEAE′是菱形？
（3）点P、Q分别以每秒2个单位和3个单位的速度同时出发，运动的时间为t秒，当t为何值时，PB∥OD？
解：（1）∵A（0，2）为抛物线的顶点，∴设y=ax2+2。
∵点C（3，0），在抛物线上，∴9a+2=0，解得：
。
∴抛物线的解析式为；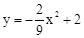
。
（2）若要四边形OEAE′是菱形，则只要AO与EE′互相垂直平分，
∴EE′经过AO的中点，∴点E纵坐标为1，代入抛物线解析式得：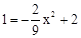
，
解得：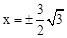
。
∵点E在第一象限，∴点E为（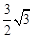
，1）。
设直线BC的解析式为y=kx+b，
把B（1，2），C（3，0），代入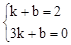得：
，解得
。
∴BC的解析式为：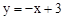
。
设直线EO的解析式为y=ax，将E点代入，可得出EO的解析式为：
。
由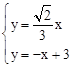
，得：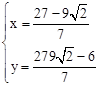
，
∴直线EO和直线BC的交点坐标为：（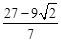
，
）。
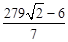∴Q点坐标为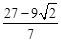：（，0）。
∴当Q点坐标为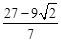（，0）时，四边形OEAE′是菱形。
（3）设t为m秒时，PB∥DO，又QD∥y轴，则有∠APB=∠AOE=∠ODQ，
又∵∠BAP=∠DQO，则有△APB∽△QDO。
∴
。
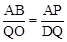由题意得：AB=1，AP=2m，QO=3﹣3m，
又∵点D在直线y=﹣x+3上，∴DQ=3m。
∴
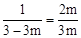，解得：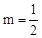
。
经检验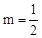：是原分式方程的解。
∴当t=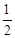
秒时，PB∥OD。
解析
练习册系列答案
名校课堂系列答案
相关题目
（b，c是常数，且c<0）与x轴分别交于点A，B（点A位于点B的左侧），与y轴的负半轴交于点C，点A的坐标为(－1，0)．
的正方形ABCD的顶点A、B在x轴上，连接OD、BD、△BOD的外心I在中线BF上，BF与AD交于点E．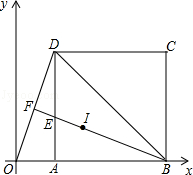
（m＞0）的图象与x轴交于A、B两点．
的顶点为点D，并与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C．
，0）和点F（0，
），直线l经过E、F两点，点G是线段BD的中点．
的图象过C点．
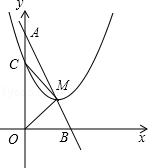
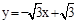与x轴、y轴分别交于A、B两点，两动点D、E分别从A、B两点同时出发向O点运动（运动到O点停止）；对称轴过点A且顶点为M的抛物线
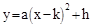（a＜0）始终经过点E，过E作EG∥OA交抛物线于点G，交AB于点F，连结DE、DF、AG、BG．设D、E的运动速度分别是1个单位长度/秒和
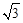个单位长度/秒，运动时间为t秒．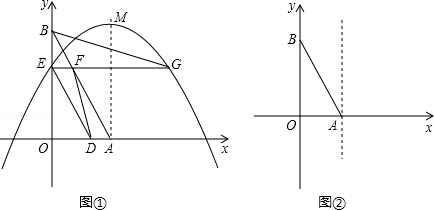
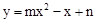的对称轴是直线x=2．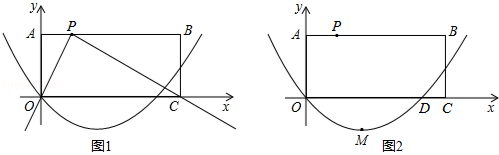
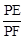的值是否发生变化？若发生变化，说明理由；若不发生变化，求出