题目内容
【题目】阅读并解决其后的问题:我们将四个有理数![]() 、
、![]() 、
、![]() 、
、![]() 写成
写成![]()
![]() 的形式,称它为由有理数
的形式,称它为由有理数![]() 、
、![]() 、
、![]() 、
、![]() 组成的二阶矩阵,称
组成的二阶矩阵,称![]() 、
、![]() 、
、![]() 、
、![]() 为构成这个矩阵的元素,如由有理数
为构成这个矩阵的元素,如由有理数![]() 、2、3、
、2、3、![]() 组成的二阶矩阵是
组成的二阶矩阵是![]()
![]() ,
,![]() 、2、3、
、2、3、![]() 是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①
是这个矩阵的元素,当且仅当两个矩阵相同位置上的元素相等时,我们称这两个二阶矩阵相等,下面是两个二阶矩阵的加法运算过程:①![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() ,②
,②![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
![]() ,
,
(1)通过观察上述例子中矩阵加法运算的规律,可归纳得二阶矩阵的加法运算法则是:两个二阶矩阵相加, .
(2)①计算:![]()
![]() +
+![]()
![]() ;
;
②若![]()
![]() +
+![]()
![]() =
=![]()
![]() ,求
,求![]() 的值;
的值;
(3)若记A=![]()
![]() ,B=
,B=![]()
![]() ,试依据二阶矩阵的加法法则说明A+B=B+A成立
,试依据二阶矩阵的加法法则说明A+B=B+A成立
【答案】(1)等于两个矩阵对应位置上的元素相加;(2)①![]() ,②x=2;(3)见解析
,②x=2;(3)见解析
【解析】
(1)根据已知的等式运算即可得到二阶矩阵的加法运算法则为:两个二阶矩阵相加,等于两个矩阵对应位置上的元素相加;
(2)①根据矩阵的加法运算法则;②根据矩阵的加法运算法则即可化简得到方程,即可求解;
(3)根据矩阵的加法运算法则即可验证.
(1)通过观察上述例子中矩阵加法运算的规律,可归纳得二阶矩阵的加法运算法则是:两个二阶矩阵相加,等于两个矩阵对应位置上的元素相加;
故填:等于两个矩阵对应位置上的元素相加;
(2)①![]()
![]() +
+![]()
![]() =
=![]()
![]() =
=![]()
②∵![]()
![]() +
+![]()
![]() =
=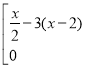
![]() =
=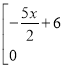
![]() =
=![]()
![]()
∴![]() =1
=1
解得x=2
(3)∵A=![]()
![]() ,B=
,B=![]()
![]()
∴A+B=![]()
![]() +
+![]()
![]() =
=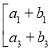
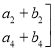
B+A=![]()
![]() +
+![]()
![]() =
=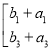
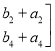 =
=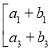
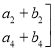
∴A+B=B+A.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目