��Ŀ����
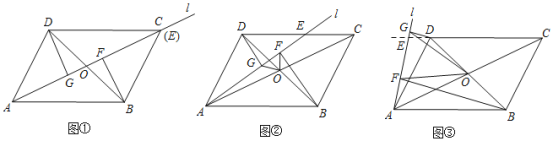
����Ŀ����֪��ֽ������һ������ͼ1�����ݸ��������ᣬ�����������⣺

��1���������ͼ��A��B�����λ�ã��ֱ�д����������ʾ����������
��2������A��B����֮��ľ����Ƕ��٣�
��3���������ϻ������A�ľ���Ϊ2�ĵ㣨�ò�ͬ��A��B��������ĸ��ʾ������д����Щ���ʾ������
��4���۵�ֽ�森���������ϩ�1��ʾ�ĵ���5��ʾ�ĵ��غϣ��ش��������⣺
��10��ʾ�ĵ������� ����ʾ�ĵ��غϣ�
����������M��N����֮��ľ���Ϊ2018��M��N����ࣩ����M��N���㾭�۵����غϣ���M��N�����ʾ�����Ƕ��٣�
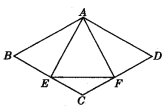
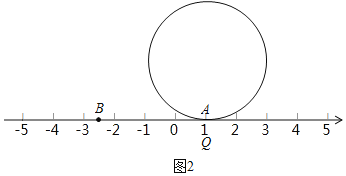
��5����ͼ2���뾶Ϊ2��Բ������һ��Q����������A�㴦����Բ�����������ҹ�����������һ�ܺ��Q������λ�õĵ�������������ʾ������
���𰸡���1��A��ʾ������1��B��ʾ�����ǩ�2.5��
��2��3.5��
��3��-1��3��
��4������6������MΪ��1007����NΪ1011��
��5��4��+1.
��������
��1��������ԭ��������Ϊ������ԭ���Ҳ����Ϊ������
��2��A��B�����ľ���ɱ�ʾΪ1-��-2.5������⼴�ɣ�
��3�����A����Ϊ2�ĵ㣬��A�������߾���������λ���ȵĵ㣬Ҳ������Ϊ1��2��1+2�ĵ㣻
��4���������-1��5���е㣬�ٸ������ĶԳ���ʽ���㼴�ɵý⣻
�������е�Ķ������MN��һ�룬Ȼ��ֱ���ʽ���㼴�ɵý⣻
��5�������Բ���ܳ����ٸ���ƽ�ƹ��ɼ��ɵó����ۣ�
�⣺��1����A��ʾ����Ϊ1����B��ʾ����Ϊ��2.5��
��2��A��B����֮��ľ���Ϊ1-��-2.5����3.5��
��3���������ϻ������A�ľ���Ϊ2�ĵ�ֱ�Ϊ3�ͩ�1����������C��D��
![]()
��4��������1+5����2��2��
2����10��2������6��
�ʴ�Ϊ����6��
�ڡ�M��N����֮��ľ���Ϊ2018��
��![]() MN��
MN��![]() ��2018��1009��
��2018��1009��
�����۵����Ϊ2��
����MΪ2��1009����1007����NΪ2+1009��1011��
��5����Բ���ܳ�=4��
�ཫԲ�����������ҹ�����������һ�ܺ��Q������λ�õĵ�������������ʾ����Ϊ4��+1��

 һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�