题目内容
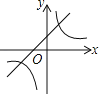
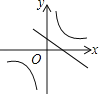
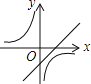
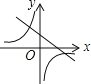
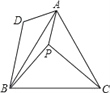
【题目】已知:如图,在等边△ABC中取点P,使得PA,PB,PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°得到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3;③∠APB=150°;
④S△APC+S△APB=![]() ,其中正确的结论有( )
,其中正确的结论有( )
A. ①②④B. ①③④C. ①②③D. ②③④
【答案】C
【解析】
由线段AP以点A为旋转中心顺时针旋转60°得到线段AD,根据旋转的性质有AD=AP,∠DAP=60°,再根据等边三角形的性质得∠BAC=60°,AB=AC,易得∠DAP=∠PAC,于是△ABD可以由△APC绕点A顺时针旋转60°得到;△ADP为等边三角形,则有PD=PA=3;在△PBD中,PB=4,PD=3,由①得到BD=PC=5,利用勾股定理的逆定理可得△PBD为直角三角形,且∠BPD=90°,则∠APB=∠APD+∠BPD=60°+90°=150°;由△ADB≌△APC得S△ADB=S△APC,则有S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD,根据等边三角形的面积为边长平方的![]() 倍和直角三角形的面积公式即可得到
倍和直角三角形的面积公式即可得到![]() 可判断④不正确.
可判断④不正确.
解:连PD,如图,
∵线段AP以点A为旋转中心顺时针旋转60°得到线段AD,
∴AD=AP,∠DAP=60°,
又∵△ABC为等边三角形,
∴∠BAC=60°,AB=AC,
∴∠DAB+∠BAP=∠PAC+∠BAP,
∴∠DAP=∠PAC,
∴△ABD可以由△APC绕点A顺时针旋转60°得到,所以①正确;
∵DA=PA,∠DAP=60°,
∴△ADP为等边三角形,
∴PD=PA=3,所以②正确;
在△PBD中,PB=4,PD=3,由①得到BD=PC=5,
∵32+42=52,即PD2+PB2=BD2,
∴△PBD为直角三角形,且∠BPD=90°,
由②得∠APD=60°,
∴∠APB=∠APD+∠BPD=60°+90°=150°,所以③正确;
∵△ADB≌△APC,
∴S△ADB=S△APC,
∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD![]() 所以④不正确.
所以④不正确.
故选:C.


【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 |
单价 | 1.4元/千米 | 0.5元/分钟 |
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。 | ||
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?
![]()