题目内容
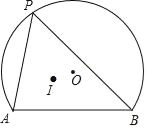
【题目】如图，AB为弓形AB的弦，AB＝2
，弓形所在圆⊙O的半径为2，点P为弧AB上动点，点I为△PAB的内心，当点P从点A向点B运动时，点I移动的路径长为_____．
【答案】
【解析】
连接OB，OA，过O作
，得到
，求得
，连接IA，IB，根据角平分线的定义得到
，
，根据三角形的内角和得到
，设A，B，I三点所在的圆的圆心为
，连接
，
，得到
，根据等腰三角形的性质得到
，连接
，解直角三角形得到
，根据弧长公式即可得到结论．
解：连接OB，OA，过O作，
，
，
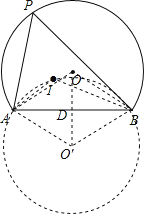
在Rt
中，
，
，
，
，
连接IA，IB，
点I为
的内心，
，，
，
，
点P为弧AB上动点，
始终等于
，
点I在以AB为弦，并且所对的圆周角为
的一段劣弧上运动，
设A，B，I三点所在的圆的圆心为，
连接，，
则，
，
，
连接，
，
，
，
点I移动的路径长
故答案为：
练习册系列答案
相关题目
