��Ŀ����
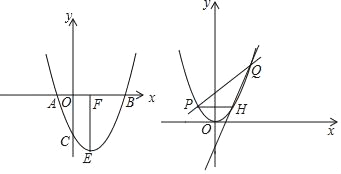
����Ŀ��������y��x2+bx+c������A��B��C����֪A����1��0����C��0����3����
��1���������ߵĽ���ʽ��
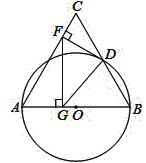
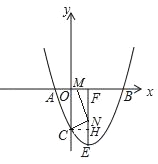
��2����ͼ1�������߶���ΪE��EF��x����F�㣬M��m��0����x����һ���㣬N���߶�EF��һ�㣬����MNC��90�㣬��ָ��ʵ��m�ı仯��Χ����˵�����ɣ�
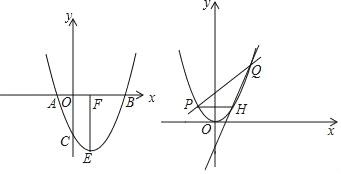
��3����ͼ2����������ƽ�ƣ�ʹ�䶥��E��ԭ��O�غϣ�ֱ��y��kx+2��k��0�����������ཻ�ڵ�P��Q����P����ߣ�������P��x��ƽ���߽��������ڵ�H����k�����ı�ʱ����˵��ֱ��QH�����㣬�������꣮
���𰸡���1��y��x2��2x��3����2��![]() ����3����k�����ı�ʱ��ֱ��QH�����㣬��������Ϊ��0����2��
����3����k�����ı�ʱ��ֱ��QH�����㣬��������Ϊ��0����2��
��������
��1���ѵ�A����1��0����C��0����3�����������߱���ʽ���b��c�����ɵó������ߵĽ���ʽ��
��2����CH��EF��H����N������Ϊ��1��n����֤��Rt��NCH�ס�MNF���ɵ�m��n2+3n+1����Ϊ��4��n��0�����ɵó�m��ȡֵ��Χ��
��3�����P��x1��y1����Q��x2��y2�������H����x1��y1������ֱ��HQ����ʽΪy��ax+t���ô���ϵ������Τ�ﶨ�������a��x2��x1��t����2�����ɵó�ֱ��QH�����㣨0����2����
�⣺��1����������y��x2+bx+c������A��C��
�ѵ�A����1��0����C��0����3�����룬�ã�![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪy��x2��2x��3��
��2����ͼ����CH��EF��H��
��y��x2��2x��3����x��1��2��4��
�������ߵĶ�������E��1����4����
��N��������1��n������4��n��0
�ߡ�MNC��90����
���CNH+��MNF��90����
�֡ߡ�CNH+��NCH��90����
���NCH����MNF��
�֡ߡ�NHC����MFN��90����
��Rt��NCH�ס�MNF��
��![]() ����
����![]()
��ã�m��n2+3n+1��![]() ��
��
�൱![]() ʱ��m��СֵΪ
ʱ��m��СֵΪ![]() ��
��
��n����4ʱ��m�����ֵ��m�����ֵ��16��12+1��5��
��m��ȡֵ��Χ��![]() ��
��
��3�����P��x1��y1����Q��x2��y2����
�߹���P��x��ƽ���߽��������ڵ�H��
��H����x1��y1����
��y��kx+2��y��x2��
��ȥy�ã�x2��kx��2��0��
x1+x2��k��x1x2����2��
��ֱ��HQ����ʽΪy��ax+t��
����Q��x2��y2����H����x1��y1�����룬��![]() ��
��
��y2��y1��a��x1+x2������k��x2��x1����ka��
��a��x2��x1��
��![]() ���� x2��x1��x2+t��
���� x2��x1��x2+t��
��t����2��
��ֱ��HQ����ʽΪy���� x2��x1��x��2��
�൱k�����ı�ʱ��ֱ��QH�����㣬��������Ϊ��0����2����

����Ŀ��2020�궫�����˻�ı�����Ʊ��ʼ���ܹ���Ԥ�����±�Ϊ���˻�ٷ�Ʊ����վ�����ļ��������������Ʊ������Ҽ۸�����С����12000Ԫ��ΪԤ���±��б�����Ŀ��Ʊ���ʽ�
������Ŀ | Ʊ��(Ԫ����) |
���� | 1000 |
���� | 800 |
ƹ���� | 500 |
(1)��ȫ���ʽ�����Ԥ��������Ʊ��ƹ������Ʊ��15�ţ���������Ʊ��ƹ������Ʊ����������?
(2)�������ʽ������ķ�Χ�ں���Ʊ�������ǰ���£����������Ԥ���ϱ�������������Ʊ������������Ʊ��ƹ������Ʊ����ͬ����������Ʊ�ķ��ò�����������Ʊ�ķ��ã��ʿ���Ԥ��������������Ʊ�������ţ�