题目内容
【题目】已知二次函数y=x2﹣2mx+m2+1(m为常数),当自变量x的值满足﹣3≤x≤﹣1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或﹣3 B. ﹣3或﹣5 C. 1或﹣1 D. 1或﹣5
【答案】D
【解析】
先找出函数对称轴,再分段讨论
由y=x2﹣2mx+m2+1(m为常数) =(x-m)2+1知,其对称轴为x=m
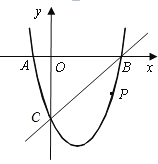
当m![]() -3时,在﹣3≤x≤﹣1上,y随x的增大而增大.所以x=-3时取得最小值y=5,
-3时,在﹣3≤x≤﹣1上,y随x的增大而增大.所以x=-3时取得最小值y=5,
即(-3-m)2+1=5,所以m=-5或-1(舍去)
当﹣3≤m≤﹣1时,函数值y的最小值为1,不符合题意.
当m![]() -1时,在﹣3≤x≤﹣1上,y随x的增大而减小.所以当x=-1时取得最小值y=5,
-1时,在﹣3≤x≤﹣1上,y随x的增大而减小.所以当x=-1时取得最小值y=5,
即(-1-m)2+1=5,所以m=1或-3(舍去)
综上所述,m的值为1或-5
故选D

练习册系列答案
相关题目