题目内容
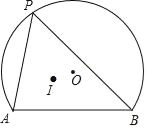
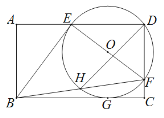
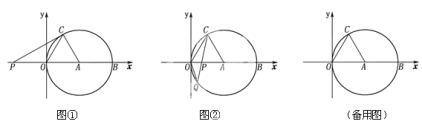
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
【答案】(1)60°.(2)4.(3)2或2+2![]() .
.
【解析】
试题(1)OA=AC首先三角形OAC是个等腰三角形,因为∠AOC=60°,三角形AOC是个等边三角形,因此∠OAC=60°;
(2)如果PC与圆A相切,那么AC⊥PC,在直角三角形APC中,有∠PCA的度数,有A点的坐标也就有了AC的长,可根据余弦函数求出PA的长,然后由PO=PA-OA得出OP的值.
(3)本题分两种情况:
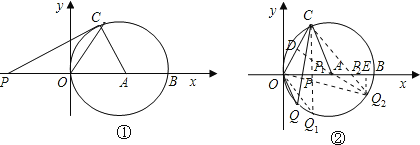
①以O为顶点,OC,OQ为腰.那么可过C作x轴的垂线,交圆于Q,此时三角形OCQ就是此类情况所说的等腰三角形;那么此时PO可在直角三角形OCP中,根据∠COA的度数,和OC即半径的长求出PO.
②以Q为顶点,QC,QD为腰,那么可做OC的垂直平分线交圆于Q,则这条线必过圆心,如果设垂直平分线交OC于D的话,可在直角三角形AOQ中根据∠QAE的度数和半径的长求出Q的坐标;然后用待定系数法求出CQ所在直线的解析式,得出这条直线与x轴的交点,也就求出了PO的值.
试题解析:(1)∵∠AOC=60°,AO=AC,
∴△AOC是等边三角形,
∴∠OAC=60°.
(2)∵CP与A相切,
∴∠ACP=90°,
∴∠APC=90°-∠OAC=30°;
又∵A(4,0),
∴AC=AO=4,
∴PA=2AC=8,
∴PO=PA-OA=8-4=4.
(3)①过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴ 弧OC=弧OQ1,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=![]() OA=2;
OA=2;
②过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2;
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∴Q2E=![]() AQ2=2,AE=2
AQ2=2,AE=2![]() ,
,
∴点Q2的坐标(4+2![]() ,-2);
,-2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴CP1=2![]() ,
,
∴C点坐标(2,2![]() );
);
设直线CQ2的关系式为y=kx+b,则
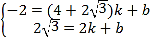 ,解得
,解得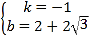 ,
,
∴y=-x+2+2![]() ;
;
当y=0时,x=2+2![]() ,
,
∴P2O=2+2![]() .
.
考点: 1.切线的性质;2.等腰三角形的性质;3.等边三角形的性质.

【题目】2020年东京奥运会的比赛门票开始接受公众预订.下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格,球迷小李用12000元做为预订下表中比赛项目门票的资金.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票共15张,问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?