题目内容
【题目】已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.
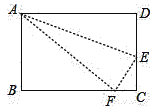
(1)当点E为边AB的中点时(如图1),求BC的长;
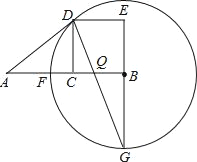
(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;
(3)当△AEF的面积为3时,求△DCE的面积.
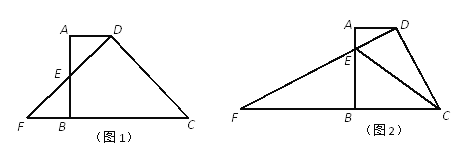
【答案】(1)9;(2)∠DCE的大小确定,![]() .(3)当△AEF的面积为3时,△DCE的面积为25或73.
.(3)当△AEF的面积为3时,△DCE的面积为25或73.
【解析】
(1)根据AD//BC和 E为AB中点,得出 AD= BF,DE= EF,再根据AD=3,AB=6,求出BF=3,再求出DF的值,最后求出CF即可;
(2)作CH⊥AD交AD的延长线于点H,再得出△AED∽△HDC再根据AB⊥AD,CH⊥AD,AD//BC,得出CH =AB=6,然后得出∠DCE的正切值;
(3)当点E在边AB上,设AE=x,根据△AEF的面积为3得出x的值,再求出DE,DC的值,然后可以得出△DCE的面积;当点E在边AB延长线上,设AE=y,根据△AEF的面积为3,得出![]() ,联结CE,作CH⊥AD交AD的延长线于点H,得出DC,DE的值即可.
,联结CE,作CH⊥AD交AD的延长线于点H,得出DC,DE的值即可.
解:(1)∵AD//BC,∴![]() .∵E为AB中点,∴AE=BE. ∴AD= BF,DE= EF.
.∵E为AB中点,∴AE=BE. ∴AD= BF,DE= EF.
∵AD=3,AB=6,∴BF=3,BE=3. ∴BF=BE.
∵AB⊥BC,∴∠F=45°且EF=![]() .
.
∴DF=2EF=![]() .
.
∵DF⊥DC,∠F=45°,∴CF=12.
∴BC= ![]() .
.
(2)∠DCE的大小确定,![]() .
.
作CH⊥AD交AD的延长线于点H,∴∠HCD+∠HDC=90°.
∵DF⊥DC,∴∠ADE+∠HDC=90°. ∴∠HCD=∠ADE.
又∵AB⊥AD,∴∠A=∠CHD. ∴△AED∽△HDC.
∴![]() .
.
∵AB⊥AD,CH⊥AD,AD//BC,∴CH =AB=6.

∵AD=3,CH=6,∴![]() .即
.即![]() .
.
(3)当点E在边AB上,设AE=x,
∵AD//BC,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∵△AEF的面积为3,∴![]() .
.
∴![]() .
.
∵AD=3,AB⊥AD,∴DE=5. ∵![]() ,∴DC=10.
,∴DC=10.
∵DF⊥DC,∴![]() .
.
当点E在边AB延长线上,设AE=y,
∵AD//BC,∴![]() ,即
,即![]() .∴
.∴![]() .
.
∵△AEF的面积为3,∴![]() .∴
.∴![]() .
.
∵AD=3,AB⊥AD,∴DE=![]() .
.
联结CE,作CH⊥AD交AD的延长线于点H,同(1)可得![]() .
.
∴DC=![]()
∵DF⊥DC,∴![]() .
.
综上,当△AEF的面积为3时,△DCE的面积为25或73.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案