题目内容
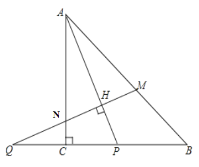
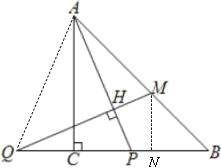
【题目】在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(1)当AP平分∠BAC时,试说明AM=AN.
(2)若∠PAC=m,求∠AMQ的大小(用含m的式子表示).
(3)用等式表示线段MB与PQ之间的数量关系,并证明.
【答案】![]() 见解析
见解析![]() ∠AMQ=45°+m.
∠AMQ=45°+m.![]()
![]()
【解析】
![]() 易证明
易证明![]() ≌
≌![]() ,根据全等三角形的性质即可证明.
,根据全等三角形的性质即可证明.
(2)QH⊥AP,AC⊥BC,∠APC=∠QPH,可得∠CAP=∠Q=m.根据等腰直角三角形的性质可得∠B=45°,根据三角形外角的性质可得∠AMQ=∠Q+∠B=45°+m.
(3)连接AQ,过点M作MN⊥BQ于N.证明△ACP≌△QNM,得到MN=CP=CQ.MN⊥BQ,∠B=45°,根据直角三角形的性质得到![]() 即可得到表示线段MB与PQ之间的数量关系
即可得到表示线段MB与PQ之间的数量关系
![]() AP平分∠BAC,
AP平分∠BAC,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
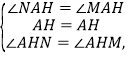
![]() ≌
≌![]() ,
,
![]()
(2)∵QH⊥AP,AC⊥BC,∠APC=∠QPH,
∴∠CAP=∠Q=m.
∵△ABC是等腰直角三角形,
∴∠B=45°,
∴∠AMQ=∠Q+∠B=45°+m.
(3)![]() .理由如下:
.理由如下:
连接AQ,过点M作MN⊥BQ于N.
∵AC⊥BC,QC=CP,
∴AQ=AP,
∴∠QAC=∠CAP=m,
∴∠QAM=∠CAB+∠QAC=45°+m=∠AMQ,
∴AQ=QM,
∴AP=QM.
∵AP=QM,∠CAP=∠MQN,∠ACP=∠QNM,
∴△ACP≌△QNM,
∴MN=CP=CQ.
∵MN⊥BQ,∠B=45°,
∴![]()
∴![]()

练习册系列答案
相关题目