题目内容
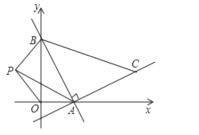
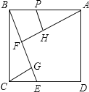
【题目】如图,在正方形![]() 中,过
中,过![]() 作一直线与
作一直线与![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,再过
,再过![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于
于![]() .若
.若![]() .则
.则![]() 与四边形
与四边形![]() 的面积之和为________.
的面积之和为________.

【答案】9
【解析】
由ABCD为正方形,根据正方形的性质得到AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又根据CG与BE垂直得到∠BCG+∠CBG=90°,根据同角的余角相等得到一对角相等,又根据一对直角相等,利用“AAS”即可得到三角形BCG与三角形FBA全等,根据全等三角形的对应边相等得到AF与BG相等,又因为FH=FB,从而得到AH=FG,然后由垂直得到一对直角相等,加上一个公共角,得到三角形APH与三角形ABF相似,根据相似得比例,设AH=FG=x,用x表示出PH,由四边形PHFB一组对边平行,另一组对边不平行得到此四边形为梯形,根据梯形的面积公式,由上底PH,下底为BF=3,高FH=3,表示出梯形的面积;然后在三角形BCG与三角形ECG中,根据同角的余角相等,再加上一对直角得到两三角形相似,根据相似得比例,用含x的式子表示出GE,由CG=3,表示出的GE,利用三角形的面积公式表示出直角三角形CGE的面积,把表示出的两面积相加,化简即可得到结论.
∵四边形ABCD为正方形,∴AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又CG⊥BE,即∠BGC=90°,∴∠BCG+∠CBG=90°,∴∠ABF=∠BCG,又AF⊥BG,∴∠AFB=∠BGC=90°,∴△ABF≌△BCG,∴AF=BG,BF=CG=FH=3.
又∵FH=BF,∴AH=FG,设AH=FG=x.
∵PH⊥AF,BF⊥AF,∴∠AHP=∠AFB=90°,又∠PAH为公共角,∴△APH∽△ABF,∴![]() =
=![]() ,即PH=
,即PH=![]() .
.
∵PH∥BF,BP不平行FH,∴四边形BFHP为梯形,其面积为![]() =
=![]() +
+![]() ;
;
又∵∠BCG+∠ECG=90°,∠ECG+∠BEC=90°,∴∠BCG=∠BEC,又∠BGC=∠CGE=90°,∴△BCG∽△CEG,∴![]() =
=![]() ,即GE=
,即GE=![]() ,故Rt△CGE的面积为
,故Rt△CGE的面积为![]() ×3×
×3×![]() ,则△CGE与四边形BFHP的面积之和为
,则△CGE与四边形BFHP的面积之和为![]() +
+![]() +
+![]() =
=![]() +
+![]() =9.
=9.
故答案为:9.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案