题目内容
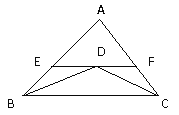
【题目】如图△ABC中，BD、CD分别平分∠ABC，∠ACB，过点D作EF//BC交AB、AC于点E、F，试说明 BE+CF=EF的理由.
【答案】见解析
【解析】
根据角平分线的定义可得：∠EBD=∠CBD，∠FCD=∠BCD，然后根据平行线的性质可得：∠EDB=∠CBD，∠FDC=∠BCD，从而证出∠EBD=∠EDB，∠FCD=∠FDC，再根据等角对等边证出：EB=ED，FD=FC，从而证出：BE+CF=EF.
解：∵BD、CD分别平分∠ABC，∠ACB，
∴∠EBD=∠CBD，∠FCD=∠BCD
∵EF//BC
∴∠EDB=∠CBD，∠FDC=∠BCD
∴∠EBD=∠EDB，∠FCD=∠FDC
∴EB=ED，FD=FC
∴BE+CF=DE+DF=EF
练习册系列答案
阅读快车系列答案
相关题目
