ΧβΡΩΡΎ»ί
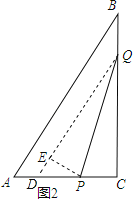
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=6cmΘ§BC=8cmΘ§ΒψP¥”A≥ωΖΔ―ΊACœρCΒψ“‘1άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·ΘΜΒψQ¥”C≥ωΖΔ―ΊCBœρBΒψ“‘2άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·Θ°ΒψPΓΔQΖ÷±π¥”ΤπΒψΆ§ ±≥ωΖΔΘ§“ΤΕ·ΒΫΡ≥“ΜΈΜ÷Ο ±Υυ–η ±ΦδΈΣtΟκΘ°

Θ®1Θ©Β±t=2 ±Θ§«σœΏΕΈPQΒΡ≥ΛΕ»ΘΜ
Θ®2Θ©Β±tΈΣΚΈ÷Β ±Θ§ΓςPCQΒΡΟφΜΐΒ»”Ύ5cm2ΘΩ
Θ®3Θ©‘ΎPΓΔQ‘ΥΕ·Ιΐ≥Χ÷–Θ§‘ΎΡ≥“Μ ±ΩΧΘ§»τΫΪΓςPQCΖ≠’έΘ§ΒΟΒΫΓςEPQΘ§»γΆΦ2Θ§PE”κABΡήΖώ¥Ι÷±ΘΩ»τΡήΘ§«σ≥ωœύ”ΠΒΡt÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() άεΟΉΘΜΘ®2Θ©Β±t=1Οκ ±Θ§ΓςPCQΒΡΟφΜΐΒ»”Ύ5cm2ΘΜΘ®3Θ©Β±t=
άεΟΉΘΜΘ®2Θ©Β±t=1Οκ ±Θ§ΓςPCQΒΡΟφΜΐΒ»”Ύ5cm2ΘΜΘ®3Θ©Β±t=![]() ±Θ§PEΓΆABΘ°
±Θ§PEΓΆABΘ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©Β±t=2 ±Θ§Ω…«σ≥ωCPΘ§CQΒΡ≥ΛΘ§ΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…«σ≥ωœΏΕΈΦ¥–±±ΏPQΒΡ≥ΛΘΜ
Θ®2Θ©”…»ΐΫ«–ΈΟφΜΐΙΪ ΫΩ…Ϋ®ΝΔΙΊ”ΎtΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σ≥ωtΒΡ÷ΒΦ¥Ω…ΘΜ
Θ®3Θ©―”≥ΛQEΫΜAC”ΎΒψDΘ§»τPEΓΆABΘ§‘ρQDΓΈABΘ§Υυ“‘Ω…ΒΟΓςCQDΓΉΓςCBAΘ§”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΘΚΕ‘”Π±ΏΒΡ±»÷ΒœύΒ»Ω…«σ≥ωDE=0.5tΘ§“Ή÷ΛΓςABCΓΉΓςDPEΘ§‘Ό”…œύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟ![]() Θ§Α―“―÷Σ ΐΨί¥ζ»κΦ¥Ω…«σ≥ωtΒΡ÷ΒΘ°
Θ§Α―“―÷Σ ΐΨί¥ζ»κΦ¥Ω…«σ≥ωtΒΡ÷ΒΘ°
ΫβΘΚΘ®1Θ©Β±t=2 ±Θ§
ΓΏΒψP¥”A≥ωΖΔ―ΊACœρCΒψ“‘1άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·ΘΜΒψQ¥”C≥ωΖΔ―ΊCBœρBΒψ“‘2άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·Θ§
ΓύAP=2άεΟΉΘ§QC=4άεΟΉΘ§
ΓύPC=4Θ§‘ΎRtΓςPQC÷–PQ=![]() =
=![]() άεΟΉΘΜ
άεΟΉΘΜ
Θ®2Θ©ΓΏΒψP¥”A≥ωΖΔ―ΊACœρCΒψ“‘1άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·ΘΜΒψQ¥”C≥ωΖΔ―ΊCBœρBΒψ“‘2άεΟΉ/ΟκΒΡΥΌΕ»‘»ΥΌ“ΤΕ·Θ§
ΓύPC=AC©¹AP=6©¹tΘ§CQ=2tΘ§
ΓύSΓςCPQ=![]() CPCQ=
CPCQ=![]() Θ§
Θ§
Γύt2©¹6t+5=0
ΫβΒΟt1=1Θ§t2=5Θ®≤ΜΚœΧβ“βΘ§…α»ΞΘ©
ΓύΒ±t=1Οκ ±Θ§ΓςPCQΒΡΟφΜΐΒ»”Ύ5cm2ΘΜ
Θ®3Θ©Ρή¥Ι÷±Θ§άμ”…»γœ¬ΘΚ
―”≥ΛQEΫΜAC”ΎΒψDΘ§
ΓΏΫΪΓςPQCΖ≠’έΘ§ΒΟΒΫΓςEPQΘ§
ΓύΓςQCPΓ’ΓςQEPΘ§
ΓύΓœC=ΓœQEP=90ΓψΘ§
»τPEΓΆABΘ§‘ρQDΓΈABΘ§
ΓύΓςCQDΓΉΓςCBAΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύQD=2.5tΘ§
ΓΏQC=QE=2t
ΓύDE=0.5t
“Ή÷ΛΓςABCΓΉΓςDPEΘ§
Γύ![]()
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚt=![]() Θ®0ΓήtΓή4Θ©Θ§
Θ®0ΓήtΓή4Θ©Θ§
Ήέ…œΩ…÷ΣΘΚΒ±t=![]() ±Θ§PEΓΆABΘ°
±Θ§PEΓΆABΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
