题目内容
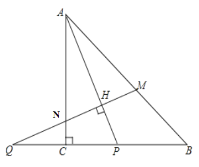
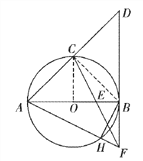
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

【答案】(1)证明见解析(2)![]()
【解析】试题分析:(1)、连接OC,根据弧的中点以及切线的性质得出OC∥BD,根据O为AB的中点得出C为AD的中点;(2)、连接BC,首先证明△COE和△FBE全等,从而得出BF=2,根据Rt△ABF的勾股定理求出AF的长度,最后根据等面积法求出BH的长度.
试题解析:(1)、连接![]() , ∵
, ∵![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 的直径, ∴
的直径, ∴![]() ,
,
∵![]() 是
是![]() 的切线, ∴
的切线, ∴![]() , ∴
, ∴![]() , ∵
, ∵![]() , ∴
, ∴![]() ;
;
(2)、连接BC, ∵![]() 是
是![]() 的中点, ∴
的中点, ∴![]() ,
,
在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() , ∵
, ∵![]() ,∴
,∴![]() , ∴
, ∴![]() ,
,
∵![]() 是直径, ∴
是直径, ∴![]() ,∴
,∴![]() , ∴
, ∴![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目