��Ŀ����
����Ŀ���ڳ�����ABCD�У�AB��8cm��BC��4cm������P�ӵ�A��������·��A��B��C�������˶����ٶ�Ϊ2cm/�룬�˶���ʱ��Ϊt��.
��1���ú�t�Ĵ���ʽ��ʾ��P�˶���·��Ϊ cm����t��4.5ʱ����P�ڱ� �ϣ�
��2������P���߶�AB���˶�ʱ��д����ADP�����S��cm2����t���룩֮��Ĺ�ϵʽ������tΪ��ֵʱ��S��8��
��3���ڵ�P�˶��Ĺ����У���ADP����״Ҳ��֮�ı䣬�жϲ�ֱ��д��tΪ��ֵʱ����ADP�ǵ��������Σ�
���𰸡���1��2t��BC����2��![]() ����
����![]() ʱ��S=8����3����
ʱ��S=8����3����![]() ��
��![]() ʱ��ADP�ǵ���������.
ʱ��ADP�ǵ���������.
��������
��1������·��=�ٶ�![]() ʱ�䣬���ɵõ��𰸣�
ʱ�䣬���ɵõ��𰸣�
��2����AD=BC=4���������ε������ʽ�����ɵõ�S��t�Ĺ�ϵʽ��Ȼ���ٰ�S=8���룬���t��ֵ���ɣ�
��3���ɡ�ADP�ǵ��������Σ��ɷ�Ϊ����������ۣ��ٵ���P��AB��ʱ��AD=AP=4���ڵ���P��BC��ʱ����AP=DP�����㼴�ɵõ���.
��1����ͼ��
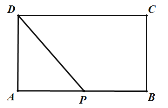
�߶���P�ӵ�A��������·��A��B��C�������˶����ٶ�Ϊ2cm/�룬�˶���ʱ��Ϊt�룬���ú�t�Ĵ���ʽ��ʾ��P�˶���·��Ϊ��![]() cm.
cm.
��t��4.5ʱ��·��Ϊ��![]() ��
��
��AB��8cm��8<9��
���Դ�ʱ��P�˶���BC�ϣ�
�ʴ�Ϊ��2t��BC��
��2�����ı���ABCD�dz����Σ�
��AD=BC=4��AP=2t��
��![]() ��
��
��S=4t����![]() ��
��
��S=8ʱ������ã�![]()
��![]() ��
��
��3���ߡ�ADP�ǵ��������Σ�
��AD=AP��AP=DP��
�ٵ���P��AB��ʱ����
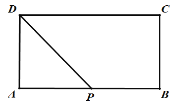
��AD=AP��
��2t=4����ã�![]() ��
��
�ڵ���P��BC��ʱ����
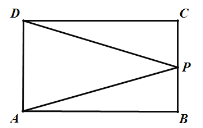
��AP=DP��
��ʱ��P��BC���е㣬
��![]() ��
��
��AB+BP=8+2=10��
���P�˶���ʱ��Ϊ��![]() s��
s��
�ۺ���������![]() ��
��![]() ʱ��ADP�ǵ��������Σ�
ʱ��ADP�ǵ��������Σ�

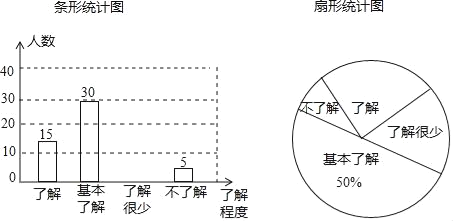
 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�