题目内容
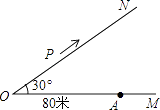
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;

(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
【答案】(1)抛物线的解析式为y=﹣x2+3x+4.(2)点P的坐标为(2,6)或(4,0).(3)△PBC的面积的最大值为8.
【解析】试题分析:(1)将点A(-1,0),B(4,0)的坐标代入抛物线的解析式,求得b、c的值即可;
(2)先由函数解析式求得点C的坐标,从而得到△OBC为等腰直角三角形,故此当CF=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4).则CF=a,PF=-a2+3a,接下来列出关于a的方程,从而可求得a的值,于是可求得点P的坐标;
(3)连接EC.设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.然后依据S△PBC=S四边形PCEB-S△CEB列出△PBC的面积与a的函数关系式,从而可求得三角形的最大面积.
试题解析:(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
![]() ,
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示:
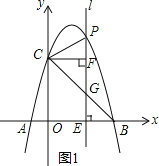
∵令x=0得y=4,
∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°,
∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC.
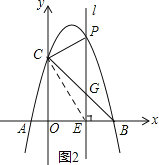
设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB=![]() OBPE=
OBPE=![]() ×4(-a2+3a+4),S△CEB=
×4(-a2+3a+4),S△CEB=![]() EBOC=
EBOC=![]() ×4×(4-a),
×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案