Question

【题目】如图，抛物线的顶点为B（-1，3），与轴的交点A在点（-3，0）和（-2，0）之间，以下结论：①；②；③；④； ⑤其中正确的有（　　）

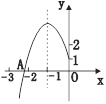
A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】B

【解析】根据二次函数的交点个数，由b2-4ac判断出①，然后根据对称性得到x=1时的函数值，判断出②，再由对称轴求出a、b的关系，判断③，根据顶点坐标求解判断④，根据根的判别式和①④的结论可判断.

抛物线与x轴有两个交点，
∴△＞0，
∴b2-4ac＞0，故①错误；
由于对称轴为x=-1，
∴x=-3与x=1关于x=-1对称，
∵x=-3时，y＜0，
∴x=1时，y=a+b+c＜0，故②错误；
∵对称轴为x=- =-1，
∴2a-b=0，故③正确；
∵顶点为B（-1，3），
∴y=a-b+c=3，
∴y=a-2a+c=3，
即c-a=3，故④正确；

当x=1时，a+b+c＜0，即a+c＜-b，

∵a＜0，x=- =-1

∴b＜0

即-b＞0

∵c-a=3，

∴c2-2ac+a2=9

∴c2+2ac+a2=9+4ac

即（a+c）2=9+4ac

∵b2-4ac＞0

∴b2＞4ac

∴与不确定，

故⑤不正确；

故选：B.