题目内容
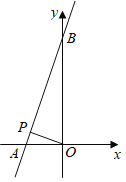
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

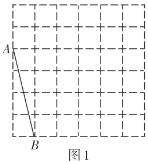
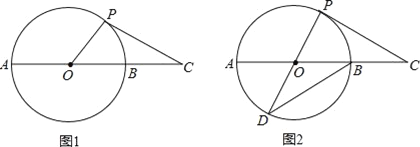
(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
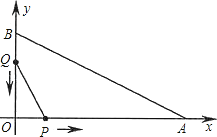
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
【答案】(1)见解析;(2)①、△BOD′∽△AOC′;(2)AC′=kBD′,∠AMB=α.
【解析】试题分析:(1)证明:在矩形ABCD中,AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC′中,
BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC′中,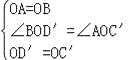 ,∴△BOD′≌△AOC′;
,∴△BOD′≌△AOC′;
(2)解:①△AOC′∽△BOD′;理由如下:∵在平行四边形ABCD中,OB=OD,OA=OC,又∵OD=OD′,OC=OC′,∴OC′=OA,OD′=OB,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴△BOD′∽△AOC′,∴BD′:AC′=OB:OA=BD:AC,∵AC=kBD,∴AC′=kBD′,∴△BOD′∽△AOC′;
②AC′=kBD′,∠AMB=α;设BD′与OA相交于点N,∴∠BNO=∠ANM,∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,即∠AMB=∠AOB=α,综上所述,AC′=kBD′,∠AMB=α.

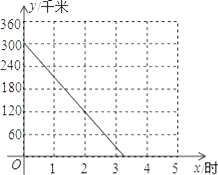
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.