题目内容
【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


【答案】(1)![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)直接利用勾股定理,即可求出AM的长度;
(2)延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .先证明
.先证明![]() ,得到
,得到![]() ,然后得到
,然后得到![]() ,再证明
,再证明![]() ,即可得到结论成立.
,即可得到结论成立.
(3)在CN上截取CE=AM,连接ME,先证明△BCE≌△ABM,然后得到△MBE为等腰直角三角形,再根据垂直平分线的性质,线段的和差关系,即可得到结论.
解:(1)∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(2)猜想:![]() .
.
证明:延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.

在![]() 和
和![]() 中,
中,
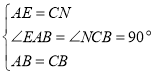 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)在CN上截取CE=AM,连接ME,

∵BC=AB,∠BAM=∠C=90°,
∴△BCE≌△BAM,
∴BE=BM,∠ABM=∠CBE,
∵∠MBN=45°,∠ABC=90°,
∴∠MBE=90°,△MBE为等腰直角三角形,
∴BN垂直ME,
∴BN为ME垂直平分线,
∴NM=NE.
∴CN-AM=CN-CE=NE=MN,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 不获奖 |
圆心角 |
|
|
|
| _________ |
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆 一等奖:双肩背包一个
二等奖:洗衣液一桶 三等奖:抽纸一盒
根据以上信息,解答下列问题:
(1)求不获奖的扇形区域圆心角度数是多少?
(2)求获得双肩背包的概率是多少?
(3)甲顾客购物520元,求他获奖的概率是多少?





