题目内容
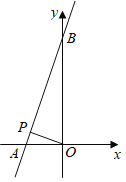
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,与
,与![]() 轴交点为
轴交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为线段
为线段![]() 上的一个动点,
上的一个动点,![]() 为坐标原点,是否存在点
为坐标原点,是否存在点![]() ,使
,使![]() 的值最小?若存在,求出
的值最小?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
【答案】(1)![]()
![]() ,
,![]()
![]() ;(2)存在,
;(2)存在,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)在一次函数![]() 中,分别令
中,分别令![]() 和
和![]() ,解相应方程,可求得A、B两点的坐标;
,解相应方程,可求得A、B两点的坐标;
(2)由垂线段最短可知当![]() 时,OP最小,利用面积法求出OP长即可.
时,OP最小,利用面积法求出OP长即可.
解:(1)![]() 一次函数
一次函数![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,![]() 点A坐标为
点A坐标为![]() ,点B坐标为
,点B坐标为![]() ;
;
(2)存在点P使得OP的值最小,理由如下:![]() 点P为线段AB上一个动点,O为坐标原点,
点P为线段AB上一个动点,O为坐标原点,![]() 当OP最小时满足
当OP最小时满足![]() ,此时OP即为
,此时OP即为![]() 中AB边上的高,
中AB边上的高,![]() 取得最小值,
取得最小值,点A坐标为
![]() ,点B坐标为
,点B坐标为![]() ,
,![]() ,
,![]() ,
,![]() 由勾股定理得:
由勾股定理得:![]() ,
,![]() 的面积
的面积![]() ,
,![]() ,
,![]() 存在点P使OP的值最小,此时
存在点P使OP的值最小,此时![]() .
.

练习册系列答案
相关题目
【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别 | 分数段(分) | 频数 | 百分率(%) |
A组 | 60≤x<70 | 30 | 10 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 40 |
D组 | 90≤x<100 | 60 | 20 |
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?