题目内容
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
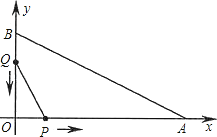
【答案】当t=4或t=2时,△POQ与△AOB相似.
【解析】试题分析:根据题意可知:OQ=6-t,OP=t,然后分![]() 和
和![]() 两种情况分别求出t的值.
两种情况分别求出t的值.
试题解析:解:①若△POQ∽△AOB时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得:12﹣2t=t,
解得:t=4.
②若△POQ∽△BOA时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得:6﹣t=2t,
解得:t=2.
∵0≤t≤6,
∴t=4和t=2均符合题意,
∴当t=4或t=2时,△POQ与△AOB相似.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目