题目内容
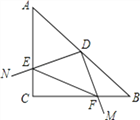
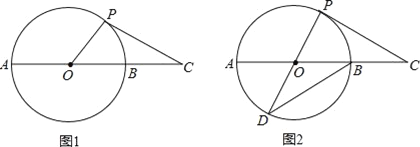
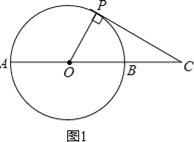
【题目】如图1,延长⊙O的直径AB至点C,使得BC=![]() AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
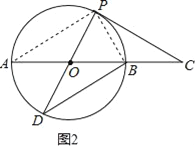
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
【答案】(1)30°;(2)有最大值为9,理由见解析;(3)证明见解析.
【解析】试题分析:(1)当PC与⊙O相切时,∠OCP的度数最大,根据切线的性质即可求得;
(2)由△OPC的边OC是定值,得到当OC边上的高为最大值时,△OPC的面积最大,当PO⊥OC时,取得最大值,即此时OC边上的高最大,于是得到结论;
(3)根据全等三角形的性质得到AP=DB,根据等腰三角形的性质得到∠A=∠C,得到CO=OB+OB=AB,推出△APB≌△CPO,根据全等三角形的性质得到∠CPO=∠APB,根据圆周角定理得到∠APB=90°,即可得到结论.
试题解析:(1)当PC与⊙O相切时,∠OCP最大.如图1,所示:
∵sin∠OCP=![]() =
=![]() =
=![]() ,∴∠OCP=30°
,∴∠OCP=30°
∴∠OCP的最大度数为30°,
故答案为:30°;
(2)有最大值,理由:
∵△OPC的边OC是定值,∴当OC边上的高为最大值时,△OPC的面积最大,
而点P在⊙O上半圆上运动,当PO⊥OC时,取得最大值,即此时OC边上的高最大,
也就是高为半径长,∴最大值S△OPC=![]() OCOP=
OCOP=![]() ×6×3=9;
×6×3=9;
(3)连结AP,BP,如图2,
在△OAP与△OBD中, 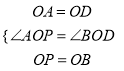 ,∴△OAP≌△OBD,∴AP=DB,
,∴△OAP≌△OBD,∴AP=DB,
∵PC=DB,∴AP=PC,
∵PA=PC,∴∠A=∠C,
∵BC=![]() AB=OB,∴CO=OB+OB=AB,
AB=OB,∴CO=OB+OB=AB,
在△APB和△CPO中, 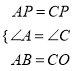 ,∴△APB≌△CPO,∴∠CPO=∠APB,
,∴△APB≌△CPO,∴∠CPO=∠APB,
∵AB为直径,∴∠APB=90°,∴∠CPO=90°,
∴PC切⊙O于点P,即CP是⊙O的切线.

【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.