题目内容
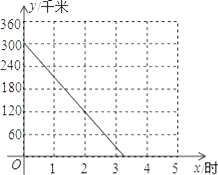
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
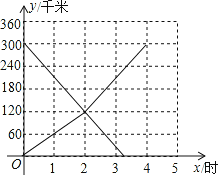
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
【答案】(1)y=-90x+300;(2)s=300-150x;(3)a=90(千米/时),作图见解析.
【解析】
试题(1)由图知y是x的一次函数,设y=kx+b.把图象经过的坐标代入求出k与b的值.
(2)根据路程与速度的关系列出方程可解.
(3)如图:当s=0时,x=2,即甲乙两车经过2小时相遇.再由1得出y=-90x+300.设y=0时,求出x的值可知乙车到达终点所用的时间.
试题解析:(1)由图知y是x的一次函数,设y="kx+b"
∵图象经过点(0,300),(2,120),
∴![]()
解得![]()
∴y=-90x+300.
即y关于x的表达式为y=-90x+300.
(2)由(1)得:甲车的速度为90千米/时,甲乙相距300千米.
∴甲乙相遇用时为:300÷(90+60)=2,
当0≤x≤2时,函数解析式为s=-150x+300,
2<x≤![]() 时,S=150x-300
时,S=150x-300
![]() <x≤5时,S=60x;
<x≤5时,S=60x;
(3)在s=-150x+300中.当s=0时,x=2.即甲乙两车经过2小时相遇.
因为乙车比甲车晚40分钟到达,40分钟=![]() 小时,
小时,
所以在y=-90x+300中,当y=0,x=![]() .
.
所以,相遇后乙车到达终点所用的时间为![]() +
+![]() -2=2(小时).
-2=2(小时).
乙车与甲车相遇后的速度a=(300-2×60)÷2=90(千米/时).
∴a=90(千米/时).
乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.

 口算能手系列答案
口算能手系列答案【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别 | 分数段(分) | 频数 | 百分率(%) |
A组 | 60≤x<70 | 30 | 10 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 40 |
D组 | 90≤x<100 | 60 | 20 |
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?