题目内容
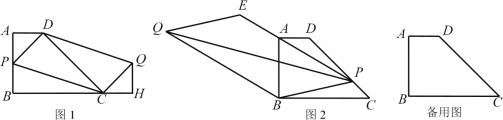
【题目】如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
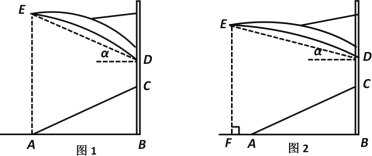
(1)求观众区的水平宽度AB.
(2)求图1中点E离水平地面的高度EA.
(3)因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)
【答案】(1)30m;(2)(![]() )m;(3)AF≈2.9m
)m;(3)AF≈2.9m
【解析】
(1)根据坡度的概念计算;
(2)过点C,D分别作CH⊥AE,DE⊥AE,垂足分别为H,G,可求得DG=30m,HG=5m,通过解直角三角形DGE,即可求出GE的长,从而解决问题;
(3)旋转后求出DG的长即可.
(1)∵AC的坡度i=1:2,BC=15 m,
∴AB=30m.
(2)如图1,过点C,D分别作CH⊥AE,DE⊥AE,垂足分别为H,G,
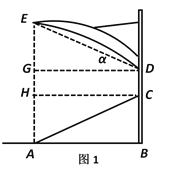
则四边形ABCH,DCHG均为矩形,
∴DG=CH=AB=30m,GH=CD=5 m,
在Rt△DGE中,DG=30m,∠GDE=30°,
∴![]()
又AH=BC=15 m,
∴EA=EG+GH+AH=(![]() )m.
)m.
(3)如图2,
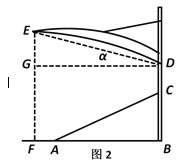
由(1)知:DE=![]() m,
m,
在Rt△DGEK中,
∵α=30°-11°30′=18°30′,
∴DG=![]() ≈32.9 m.
≈32.9 m.
∵DG=BF
∴AF=BF-AB≈32.9-30=2.9m.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目