题目内容
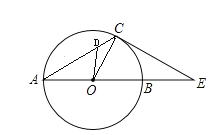
【题目】若三角形的一条角平分线与被平分的角的一边相等,则称这个三角形为“弱等腰三角形”,这条角平分线叫做这个三角形的“弱线”,如图①,AD是△ABC的角平分线,当AD=AB时,则△ABC是“弱等腰三角形”,线段AD是△ABC的“弱线”.
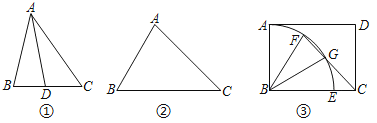
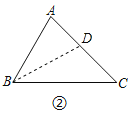
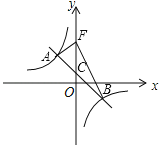
(1)如图②,在△ABC中.∠B=60°,∠C=45°.求证:△ABC是“弱等腰三角形”;
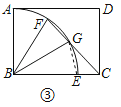
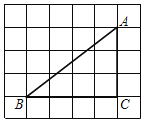
(2)如图③,在矩形ABCD中,AB=3,BC=4.以B为圆心在矩形内部作![]() ,交BC于点E,点F是
,交BC于点E,点F是![]() 上一点,连结CF.且CF与
上一点,连结CF.且CF与![]() 有另一个交点G.连结BG.当BG是△BCF的“弱线”时,求CG的长.
有另一个交点G.连结BG.当BG是△BCF的“弱线”时,求CG的长.
(3)已知△ABC是“弱等腰三角形”,AD是“弱线”,且AB=3BD,求AC:BC的值.
【答案】(1)见解析;(2)2;(3)24:17
【解析】
(1)根据角平分线的定义得到∠DBC=![]() ∠ABC=30°,根据三角形的内角和得到∠A=180°﹣∠ABC﹣∠C=180°﹣60°﹣45°=75°,于是得到结论;
∠ABC=30°,根据三角形的内角和得到∠A=180°﹣∠ABC﹣∠C=180°﹣60°﹣45°=75°,于是得到结论;
(2)如图③,连接EG,根据角平分线的定义得到∠FBG=∠GBE,根据全等三角形的性质得到∠BGF=∠BGE,根据相似三角形的性质即可得到结论;
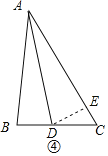
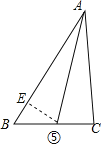
(3)①如图④,当AB=AD时,在AC上取一点E,使得AE=AB,连接DE,根据角平分线的定义得到∠FBG=∠GBE,根据全等三角形的性质得到∠BGF=∠BGE,根据相似三角形的性质即可得到结论;②当AC=AD时,如图⑤,在AB上取一点E,使AE=AC,连接DE,同理可得结论.
(1)证明:如图②作△ABC的角平分线BD,交AC于D,
∴∠DBC=![]() ∠ABC=30°,
∠ABC=30°,
∵∠ABC=60°,∠C=45°,
∴∠A=180°﹣∠ABC﹣∠C=180°﹣60°﹣45°=75°,
∵∠ADB=∠DBC+∠C=30°+45°=75°,
∴∠ADB=∠A,
∴BA=BD,
∴△ABC是“弱等腰三角形”;
(2)如图③,连接EG,
∵BG是△BCF的“弱线”,
∴BG平分∠FBC,
∴∠FBG=∠GBE,
∵BF=BE,BG=BG,
∴△BGF≌△BGE(SAS),
∴∠BGF=∠BGE,
∵BG=BE,
∴∠BGE=∠BEG=![]() (180°﹣∠GBE),
(180°﹣∠GBE),
∴∠FGE=180°﹣∠GBE,
∵∠CGE=180°﹣∠FGE,
∴∠CGE=∠CBG,
∵∠GCE=∠BCG,
∴△GCE∽△BCG,
∴![]() =
=![]() ,
,
∵CE=4﹣3=1,
∴CG2=CEBC=1×4=4,
∴CG=2;
(3)①如图④,当AB=AD时,在AC上取一点E,使得AE=AB,连接DE,
∵AD是“弱线”,
∴AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵AD=AD,
∴△ABD≌△AED(SAS),
∴DE=BD,∠B=∠AED,
∵AD=AB,
∴∠B=∠ADB,
∴∠AED=∠ADB,
∴∠CED=180°﹣∠AED,∠ADC=180°﹣∠ADB,
∴∠CED=∠ADC,
∵∠C=∠C,
∴△ADC∽△DEC,
∴![]() =
=![]() ,
,
∴CE=![]() CD,CD=
CD,CD=![]() AC,
AC,
∴CE=![]() AC,
AC,
∴CE=![]() AE=
AE=![]() BD,CD=3CE=
BD,CD=3CE=![]() BD,
BD,
AC=9CE=![]() BD,
BD,
∴BC=BD+![]() BD=
BD=![]() BD,
BD,
∴AC:BC=27:17;
②当AC=AD时,如图⑤,在AB上取一点E,使AE=AC,连接DE,
同理可得, ![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,由上面计算可得,BC=
,由上面计算可得,BC=![]() CD,
CD,
∵AC=3CD,
∴AC:BC=24:17.