题目内容
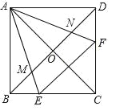
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,
边上,![]() ,连接
,连接![]() ,若
,若![]() ,则线段
,则线段![]() 的长为______.
的长为______.
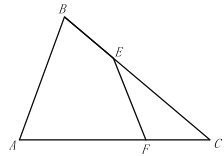
【答案】5
【解析】
过点B作BG∥AC,过点F作FG∥AB交CB于H,过点E作EM⊥FG,则ABGF为平行四边形,根据已知可得EC=AF=BG,∠A=∠ABC,易证△CFE≌△BEG,∠A=∠EHG,可得EF=EG,进而得到∠A-∠CEF=∠ABC-∠CEF=∠EHG-∠CEF=∠EFG,则![]() ,而
,而![]() ,可得EM=3,再根据勾股定理求得EF=5.
,可得EM=3,再根据勾股定理求得EF=5.
解:如图,过点B作BG∥AC,过点F作FG∥AB交CB于H,过点E作EM⊥FG,
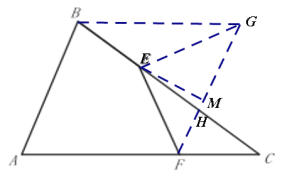
∴ABGF为平行四边形,∠C=∠GBC,
∴BG=AF,∠ABC =∠BHG,
∵![]() ,
,![]() ,
,
∴CE=AF,∠A=∠ABC,
∴CE=BG,∠A=∠EHG,
∴△CFE≌△BEG,
∴EF=EG,
∴点M为FG中点,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:5.

练习册系列答案
相关题目