题目内容
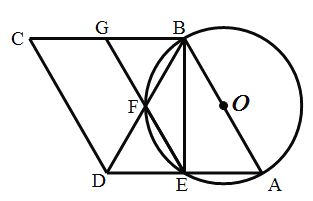
【题目】如图,在菱形ABCD中,∠BAD=60°,以AB为直径的⊙O分别交边AD和对角线BD于点E、F,连接EF并延长交边BC于点G,连接BE。
(1)求证:AE=DE;
(2)若⊙O的半径为2,求EG的长
【答案】(1)详见解析;(2)4.
【解析】
(1)先证明△ABD为等边三角形,再根据AB为直径得到BE⊥AD,利用三线合一即可求解;
(2)证明四边形ABGE为平行四边形,得到EG=AB即可求解.
(1)∵四边形ABCD为菱形,
∴AD=AB,
∵∠BAD=60°
∴△ABD为等边三角形,
∴AB=BD,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BE⊥AD,
∴AE=DE;
(2)∵四边形ABFE是圆内接四边形,
∴∠FBA+∠FEA=180°,
∵△ABD为等边三角形,
∴∠FBA=∠BAE=60°,
∴∠BAE+∠FEA=180°,
∴AB∥EG,
∵四边形ABCD为菱形,
∴AD∥BC,
∴四边形ABGE为平行四边形
∴EG=AB=2r=4.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目