题目内容
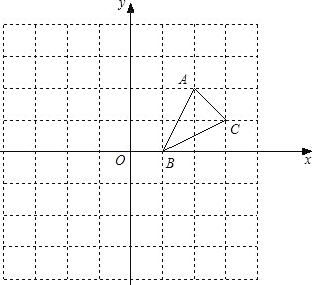
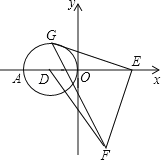
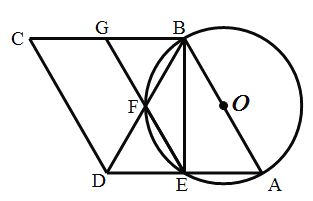
【题目】已知,如图,点D是等边三角形ABC的外接圆上的一点,过点D作圆的切线,交BC的延长线于F.
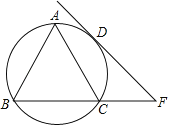
(1)用尺规作图,作出等边三角形ABC外接圆的圆心O;
(2)若⊙O的半径为2,∠F=45°,求CF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)作出AC,BC边上的高所在的直线,两直线交于点O,点O即为所求.
(2)连接DO并延长交BC于G,AO交BC于H,根据CF=GF﹣GH﹣HC,求出GF,CH,GH即可.
(1)作图点O如图所示.
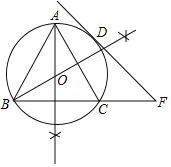
(2)连接DO并延长交BC于G,设AO交BC于H.
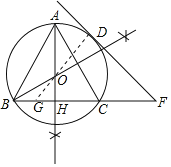
∵点O是△ABC外接圆的圆心,
∴AH是BC的垂直平分线,BO平分∠ABC,OB是⊙O的半径,
∵△ABC是等边三角形,
∴∠OBH=30,
∴OH=![]() OB=1,
OB=1,
∴在Rt△OBH中,BH=![]() ,
,
∴CH=BH=![]() ,
,
∵DF是⊙O的切线,
∴∠GDF=90°,
∵∠F=45°,
∴△DGF,△OGH是等腰直角三角形,
∴GH=OH=1,
∴在Rt△OGH中,OG=![]() ,
,
∴DF=DG=DO+GO=2+![]() ,
,
∴在Rt△DGF中,GF=![]() ,
,
∴CF=GF﹣GH﹣HC=![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】创客联盟的队员想用3D的打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
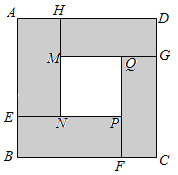
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1700元购买材料一定够用吗?请说明理由.