题目内容
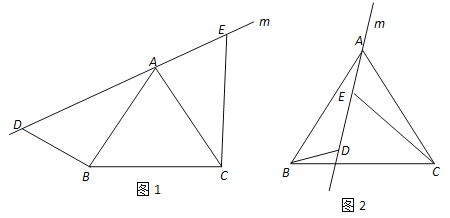
【题目】探索与证明：（1）如图1，直线m经过正三角形ABC的顶点A，在直线m上取两点 D，E，使得∠ADB=60°，∠AEC=60°．通过观察或测量，猜想线段BD，CE与DE之间满足的数量关系，并予以证明；
（2）将（1）中的直线m绕点A逆时针方向旋转一个角度到如图2的位置，并使∠ADB=120°，∠AEC=120°．通过观察或测量，请直接写出线段BD，CE与DE之间满足的数量关系．
【答案】(1)BD+CE=DE，证明见解析；（2）BD+DE=CE
【解析】试题分析：（1）通过证明△DAB≌△ECA（AAS），得出AD=CE，BD=AE，进而证得BD+CE= DE：
（2）通过△DAB≌△ECA（AAS），得出AD=CE，BD=AE，从而证得CE-BD=DE．
解：(1)猜想：BD+CE=DE.
证明：由已知条件可知：
∠DAB+∠CAE=120°,∠ECA+∠CAE=120°，
∴∠DAB=∠ECA.
在△DAB和△ECA中,
，
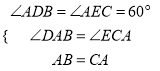∴△DAB≌△ECA(AAS).
∴AD=CE，BD=AE.
∴BD+CE=AE+AD=DE.
(2)猜想：CEBD=DE.
证明：由已知条件可知：
∠DAB+∠CAE=60°,∠ECA+∠CAE=60°，
∴∠DAB=∠ECA.
在△DAB和△ECA中,
，
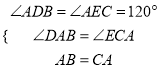∴△DAB≌△ECA(AAS).
∴AD=CE，BD=AE.
∴CEBD=ADAE=DE.
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
【题目】某企业车间有50名工人，某一天他们生产的机器零件个数统计如表：
零件个数（个） | 6 | 7 | 8 |
人数（人） | 15 | 22 | 10 |
表中表示零件个数的数据中，众数、中位数分别是（ ）
A.7个、7个B.6个、7个C.5个、6个D.8个、6个
