题目内容
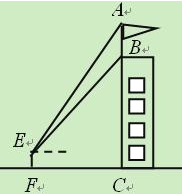
【题目】如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小明的观测点与地面的距离EF为.6m.
⑴求建筑物BC的高度;
⑵求旗杆AB的高度.(结果精确到0.1m.参考数据:![]() ≈1.41,sin52°≈0.79,tan52°≈1.28)
≈1.41,sin52°≈0.79,tan52°≈1.28)
【答案】(1)建筑物BC的高度为13.6m.
(2)旗杆AB的高度约为3.4m.
【解析】
(1)先过点E作ED⊥BC于D,由已知底部B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC.
(2)由已知由E点观测到旗杆顶部A的仰角为52°可求出AD,则AB=AD-BD.
解:(1)过点E作ED⊥BC于D,
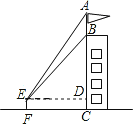
根据题意得:EF⊥FC,ED∥FC,
∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BED=45°,
∴∠EBD=45°,
∴BD=ED=FC=12,
∴BC=BD+DC=BD+EF=12+1.6=13.6,
答:建筑物BC的高度为13.6m.
(2)已知由E点观测到旗杆顶部A的仰角为52°,即∠AED=52°,
∴AD=EDtan52°
≈12×1.28≈15.4,
∴AB=AD-BD=15.4-12=3.4.
答:旗杆AB的高度约为3.4m.

练习册系列答案
相关题目