题目内容
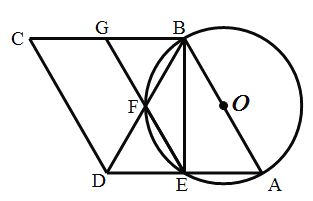
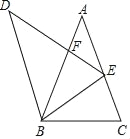
【题目】如图，在△ABC中，∠A=36°，AC=AB=2，将△ABC绕点B逆时针方向旋转得到△DBE，使点E在边AC上，DE交AB于点F，则△AFE与△DBF的面积之比等于（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
先证明△AEF∽△BDF，从而
,设DB=DE=AB=AC=y，BC=BE=AE=x，由△CBE∽△CAB，得BC2=CE·CA，代入x和y ，即可求出
的值，从而可求出结论.
∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
∵BC=BE，
∴∠C=∠BEC=72°，
∴∠EBC=36°，
∴∠ABE=∠A=36°，
∴AE=BE，
∴BC=BE=AE.
∵∠DBE=72°，
∴∠ABD=∠A=36°，
∴BD∥AE，
∴△AEF∽△BDF，
∴，
设DB=DE=AB=AC=y，BC=BE=AE=x，
∵∠C=∠C，∠CBE=∠A，
∴△CBE∽△CAB，
∴BC2=CE·CA，
∴x2=（y﹣x）y，
∴x2+xy﹣y2=0，
∴x=
y，或x=
y，
∴=，
∴
=（
）2=
.
故选：C．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
