Question

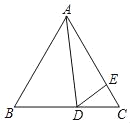
【题目】如图，∠ABD＝∠BCD＝90°，ABCD＝BCBD，BM∥CD交AD于点M．连接CM交DB于点N．

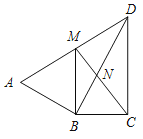
（1）求证：△ABD∽△BCD；

（2）若CD＝6，AD＝8，求MC的长．

Answer 1

【答案】（1）见解析；（2）MC＝2.

【解析】

（1）由两组边成比例，夹角相等来证明即可；

（2）由相似三角形的性质得边成比例，进而利用勾股定理求得BC，再判定∠MBC＝90°，最后由勾股定理求得MC的值即可．

（1）证明：∵ABCD＝BCBD

∴＝

在△ABD和△BCD中，∠ABD＝∠BCD＝90°

∴△ABD∽△BCD；

（2）∵△ABD∽△BCD

∴＝，∠ADB＝∠BDC

又∵CD＝6，AD＝8

∴BD2＝ADCD＝48

∴BC＝＝＝2

∵BM∥CD

∴∠MBD＝∠BDC，∠MBC＝∠BCD＝90°

∴∠ADB＝∠MBD，且∠ABD＝90°

∴BM＝MD，∠MAB＝∠MBA

∴BM＝MD＝AM＝4

∴MC＝＝＝2．