题目内容
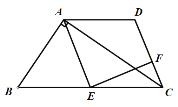
【题目】如图，在□ABCD中，点E是边AD上一点，且AE=AB．
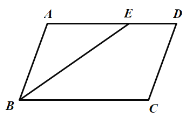
（1）作∠BCD的角平分线CF，交AD于F点，交BE于G点；（尺规作图，保留痕迹，不写画法）
（2）在（1）的条件下，
①求∠BGC的度数；
②设AB=a，BC=b，则线段EF= （用含a,b的式子表示）；
③若AB=10，CF=12，求BE的长．
【答案】（1）见解析；（2）①90°；②
；③ 
【解析】
（1）以点D为圆心，DC为半径作圆交AD于点F，连接CF交BE于点G即为所作；
（2）①根据角平分线的定义和平行线的性质，就可求出；
②根据角平分线的定义和平行线的性质可得出DC=DF，再因为AB=AE即可求出；
③根据平行线+角平分线可推出等腰三角形，进而可证得四边形AHCF是平行四边形，因为∠BGC=90°可得∠AMB=90°，所以点M是BE的中点也是AH的中点，再根据勾股定理可求出BM的值，即可求出答案．
（1）如下图所示：
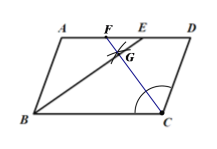
此图即为所作．
（2）①∵AB=AE，
∴∠ABE=∠AEB，
∵四边形ABCD是平行四边形，
∴AD∥BC，∠ABC+∠BCD=180°，
∴∠AEB=∠CBE，
∴∠ABE=∠CBE=
∠ABC，
∵CF平分∠BCD，
∴∠BCF=∠BCD，
∴∠CBE+∠BCF=90°，
∴∠BGC=180°-90°=90°
②∵CF平分∠BCD，
∴∠BCF=∠DCF
∵AD∥BC，
∴∠BCF=∠DFC，
∴∠DFC=∠DCF，
∴DF=DC，
∵AB=a，BC=b，
∴EF=，
③作∠BAD的平分线交BC于点H，交BE于点M，如下图所示：
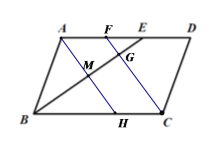
∵AH平分∠BAD，
∴∠BAH=∠DAH,
∵AD∥BC，
∴∠BAH=∠AHB，
∴AB=BH，△ABH是等腰三角形，
∵DC=DF,
∴BH=DF
∴HC=BC-BH=AD-DF=AF，
∵AD∥BC，
∴四边形AHCF是平行四边形，
∴AH∥CF，
∴∠BMH=∠BGC=90°，
∴点M是AH的中点，
∵AB=AE，
∴△ABE是等腰三角形，
∴点M是BE的中点，
∵AB=10，CF=12，
∴AH=CF=10，
∴AM=6，
在△AMB中，由勾股定理得：
,
∴BE=16．
