��Ŀ����
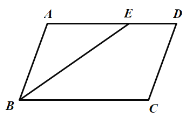
����Ŀ����ͼ��̽������д������������ͼ�ۼ������� 0.5 ����ɫǩ�ֱ�����ۼ��� ��ͼ����DBC �͡�ECB ����ABC �����������
(1)��ֱ�ߺ�Բ��ֱ�����DBC �͡�ECB ��ƽ���ߣ��������ཻ�ڵ� P��
(2)���� P �ֱ�ֱ�� AB��AC��BC �Ĵ��߶� PM��PN��PQ������ Ϊ M��N��Q��
(3) PM��PN��PQ ����𣿣�ֱ��д�����ۣ�����˵�����ɣ�

���𰸡���1����������2����������3��֤��������
��������
��1����2����Ҫ����ͼ���ɣ�
��3��PM��PN��PQ��Ȼ����ȵģ��ڡ�DBC�У�����BP�ǡ�DBC�Ľ�ƽ���ߣ�����P������BP�ϣ���PM��PQ�ֱ�ֱ�ڡ�DBC�����ߣ����ݽ�ƽ���ߵ����ʣ����ɵ�PM=PQ��ͬ����֤PN=PQ���ɴ˵õ�����Ľ���
(1)����ͼ��
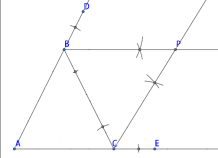
(2)����ͼ��
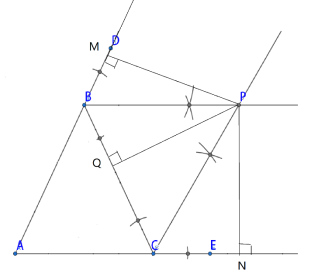
��3��PM=PN=PQ��
���ɣ�����BP�ǡ�DBC�Ľ�ƽ���ߣ���PM��BD��PQ��BC�����ݽ�ƽ���ߵ����ʵã�PM=PQ��ͬ����PQ=PN��
��PM=PN=PQ

��ϰ��ϵ�д�
�����Ŀ