题目内容
【题目】在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() .
.
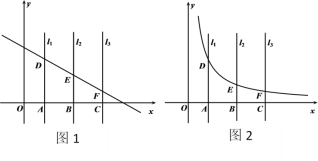
(1)如图1,若直线![]() 与直线
与直线![]() ,
,![]() ,
,![]() 分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(![]() ,
,![]() ),E(
),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ) .
) .
①若![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() (填“=”,“>”或“<”);
(填“=”,“>”或“<”);
②若![]() ,
,![]() ,
,![]() (
(![]() ),求证:AB=BC;
),求证:AB=BC;
(2)如图2,点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),直线
),直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索
![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①根据点D、E、F的横坐标证得AB=BC=1,过点E作EM⊥AD,过点F作FN⊥BE,证明△DME≌△ENF,得到DM=EN,即可推出![]() ,由此得到答案;
,由此得到答案;
②过点E作EM⊥AD,过点F作FN⊥BE,得到![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,
,![]() (
(![]() ),证得DM=EN,证明△DME≌△ENF即可推出AB=BC;
),证得DM=EN,证明△DME≌△ENF即可推出AB=BC;
(2)连接直线DF交直线![]() 于G,根据点A,B,C的横坐标分别为
于G,根据点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),得到AB=BC,D(n-1,
),得到AB=BC,D(n-1,![]() ),E(n,
),E(n,![]() ),F(n+1,
),F(n+1,![]() ),由(1)得到
),由(1)得到![]() ,由直线
,由直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,求得
)的图像分别交于点D,E,F,求得![]() ,
,![]() ,根据点G的纵坐标大于点E的纵坐标,点E的纵坐标为
,根据点G的纵坐标大于点E的纵坐标,点E的纵坐标为![]() ,得到
,得到![]() ,即可推出
,即可推出![]() .
.
(1)①∵D(1,![]() ),E(2,
),E(2,![]() ),F(3,
),F(3,![]() ),且过点A,B,C分别作与
),且过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() ,
,
∴A(1,0),B(2,0),C(3,0),
∴AB=BC=1,
过点E作EM⊥AD,过点F作FN⊥BE,
∴∠DME=ENF=90°,
∵![]() ∥
∥![]() ,
,
∴∠EDM=∠FEN,
∴△DME≌△ENF,
∴DM=EN,
∴![]() ,
,
∴![]() ,
,
故答案为:=;
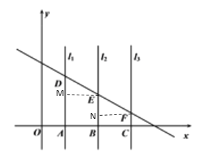
②过点E作EM⊥AD,过点F作FN⊥BE,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() (
(![]() ),
),
∴DM=2,EN=2,
∴DM=EN,
∵![]() ∥
∥![]() ,
,
∴∠EDM=∠FEN,
∵∠DME=ENF=90°,
∴△DME≌△ENF,
∴AB=BC;
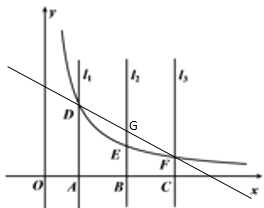
(2)![]() ,
,
连接直线DF交直线![]() 于G,
于G,
∵点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),
),
∴点D,G,F的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),AB=BC,
),AB=BC,
∴D(n-1,![]() ),E(n,
),E(n,![]() ),F(n+1,
),F(n+1,![]() ) ,
) ,
∴![]() ,
,
∵直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,
)的图像分别交于点D,E,F,
∴![]() ,
,![]() ,
,
又∵点G的纵坐标大于点E的纵坐标,点E的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() .
.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 |
频数 | 1 | 2 | 25 |
次数 | 120≤x<140 | 140≤x<160 | 160≤x<180 |
频数 | 15 | 5 | 2 |
(1)全班有多少学生?
(2)组距是多少?组数是多少
(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?