��Ŀ����
����Ŀ����һ�������Ĵ�����װ�г���ɫ�ⶼ��ͬ�ĺ���ͻ���������ɫ����һ����10����ÿ����������һ��������ɫ�Żؽ��ȣ�һ��ͬѧ�����˷������飬���������������õ����ݣ�
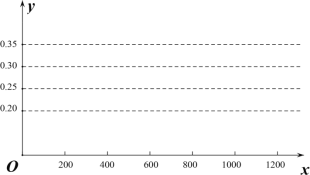
��1��a= ���������������Ƶ�ʵ�����ͳ��ͼ��
��2�������������������һ������������ĸ��ʹ���ֵ�Ƕ��٣�����ȷ��0.1��
��3�������ı���к�������ĸ���������ʹ��������һ�Σ�����������ɫ��ĸ�����ȣ���д��һ�ַ������ɣ�
���𰸡���1��![]() ����2��ԼΪ0.7����3������4��������õ�4�����𰸲�Ψһ��
����2��ԼΪ0.7����3������4��������õ�4�����𰸲�Ψһ��
��������
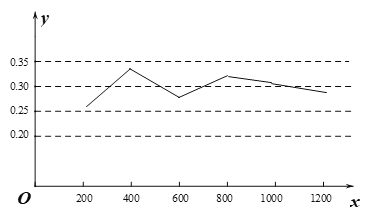
��1����������ֻҪ��348����1200����a��ֵ�������ɻ������������Ƶ�ʵ�����ͳ��ͼ��
��2���ɱ������ݿɵ�����������ʵĹ���ֵ�������ɵ���������ĸ��ʹ���ֵ��
��3������ǰ��ȷ�������к���ͻ���ĸ�������������x�����������y�������������г����̣��ⷽ�̼��ɵó����ۣ�
�⣺��1��348��1200=0.29����![]() ��
��
���������Ƶ�ʵ�����ͳ��ͼ��ͼ��ʾ��
��2��������ã�����������ʵĹ���ֵΪ0.3��������������ĸ��ʹ���ֵ=1��0.3=0.7��
��3�����ڴ������к���3��������7������������x��������![]() ����ã�x=4��
����ã�x=4��
��������y��������![]() ����ã�y=4��
����ã�y=4��
��������4��������õ�4�����𰸲�Ψһ��������ʹ��������һ�Σ�����������ɫ��ĸ�����ȣ�

����Ŀ������ίԱͳ����ȫ��ͬѧ60�������Ĵ���,���г������Ƶ���ֲ�
���� | 60��x<80 | 80��x<100 | 100��x<120 |
Ƶ�� | 1 | 2 | 25 |
���� | 120��x<140 | 140��x<160 | 160��x<180 |
Ƶ�� | 15 | 5 | 2 |
(1)ȫ���ж���ѧ��?
(2)����Ƕ���?�����Ƕ���
(3)��������x��100��x<140��Χ��ѧ��ռȫ��ѧ���İٷ�֮��?
(4)�����ʵ���ͳ��ͼ��ʾ�������Ϣ.
(5)���������������������ɼ�?